The pairing mechanism in the cuprate superconductors remains unresolved up to date. In a conventional superconductor, there is a superconducting gap in the superconducting state because of the pairing and condensation of the electrons. The gap can protect the superfluid of the superconducting state at finite temperature, and consequently the behaviors of zero resistance and diamagnetization emerge. In sharp contrast, the so-called pseudogap can appear above T_c in the underdoped region of the cuprate superconductors, while the bulk superconducting feature begins to appear in a lower temperature (see Fig. 1). Many models were proposed to interpret the mechanism of these features. One scenario assumes that the pseudogap reflects only a competing or coexisting order of superconductivity and it may have nothing to do with the pairing. And the superconducting transition still satisfies the Bardeen-Cooper-Schrieffer (BCS) picture. However, other pictures consider that the pseudogap corresponds to the energy scale of the electron-pairing intensity and the preformed Cooper pairs appear above T_c. The superconducting transition temperature is determined by the phase stiffness rather than the electron-pairing strength, since the concentration of the superfluid is rather low. As a result, the superconducting transition will not satisfy the BCS picture any more. Experimentally, some evidence for fluctuating superconductivity in the normal state of underdoped samples has been inferred in some measurements, such as the Nernst effect. The evidence from entropy, which reflects the bulk property of samples, for this residual superconductivity in the normal state is, however, still lacking.

　  Entropy is a basic physical quantity which measures the degree of disorder a physical system. It will be very convincing for a phase transition process if we can detect it from the entropy. Entropy is a quantity concerning only the state, so it has nothing to do with the virtue process . In a conventional superconductor, for example, the entropy measured along the path of superconducting state will be equal to that measured along the path of normal state, which can be achieved by destroying the superconducting state with a high magnetic field. This is what we called the entropy conservation. However, it is quite difficult to measure the superconductivity related entropy in the cuprate superconductors. The reasons are as following. Firstly, the relatively low magnetic field (about 10 T) in the usual laboratory cannot suppress the bulk superconductivity completely because of the very high upper critical field in those samples. Secondly, the superconductivity related entropy is too small, so it’s difficult to detect. Consequently, we have to obtain high-quality single crystals with low transition temperatures, where the superconductivity can be killed by the magnetic fields in the usual laboratory, and enhance the resolution of specific heat measurement, in order to detect the entropy changing in the cuprate superconductors. Loram’s group in UK and Junod group in Switzerland have measured the electronic specific heat of cuprate superconductors carefully. However, no report can be found about the difference of entropy between before and after the superconductivity is suppressed.
　  Wen et al. from SC1 group in Institute of Physics have investigated in-depth the properties of the low-energy quasiparticle excitations of the unconventional superconductors in recent years. They have grown systematically doped Bi₂Sr_2-xLaxCuO₆ (Bi-2201) single crystals with high quality. This system has a rather low T_c and it is easy to suppress the superconductivity with low fields [see J. of Crys. Growth 305 (2007) 222; Supercond. Sci. Technol. 21 (2008) 125024; Phys. Rev. Lett. 101, 207002 (2008)]. In addition, they enhanced the resolution and reduced the system error in measuring the specific heat [see Phys. Rev. B 70, 214505(2004); Phys. Rev. B 72, 134507(2005); Phys. Rev. B 76, 064512(2007); PNAS 104, 15259 (2007); Phys. Rev. B 79, 174501 (2009)]. On the basis of two conditions mentioned above, they have measured superconductivity related entropy on Bi₂Sr_2-xLaxCuO₆ single crystals successfully. For the first time, they give the evidence that the BCS picture cannot describe the cuprate superconductors in the underdoped region from the entropy point of view, which means that part of the electron Cooper pairs are already present in the normal state and the superconducting transition is corresponding to the establishment of the phase coherence.
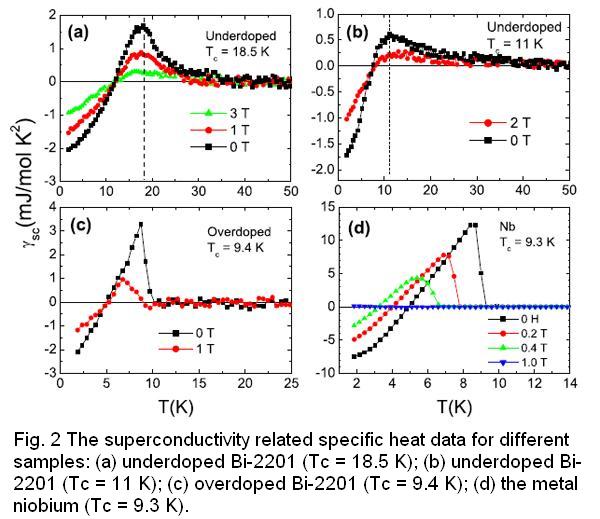
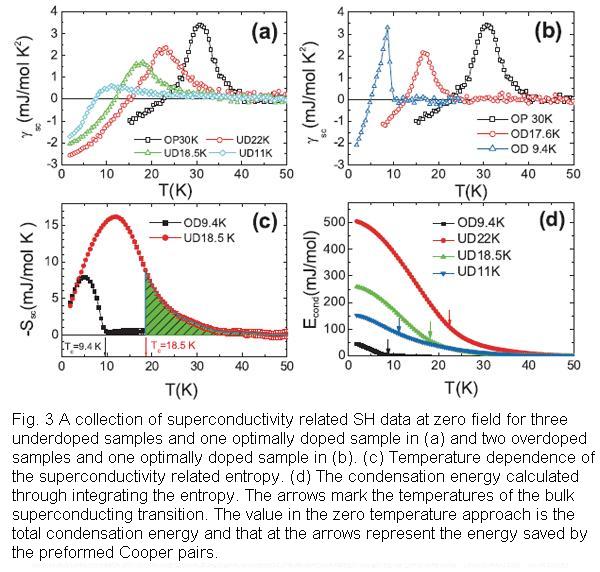
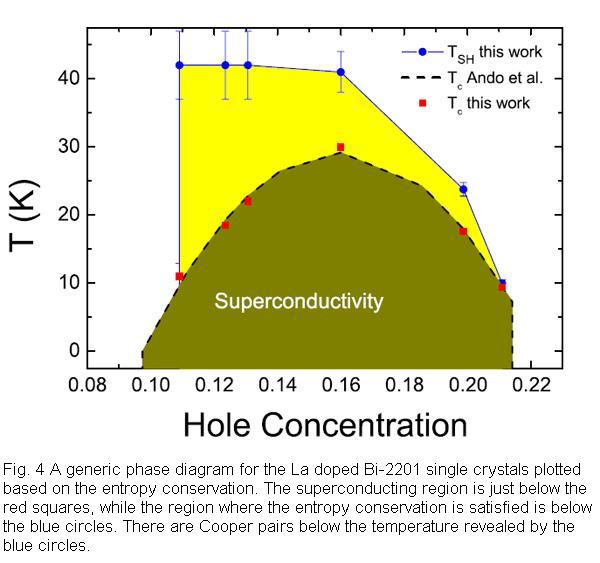
　  The typical results are shown in Fig. 2. Figure 2 (a), (b), and (c) represent the specific heat (SH) data related to superconductivity of two underdoped and one overdoped Bi-2201 samples, respectively, while Fig. 2(d) shows that of the metal niobium (Nb). One can see that the SH jump because of the superconducting transition is rather sharp for the heavy overdoped samples and consequently the entropy conservation can be achieved at the superconducting transition point (see Fig. 3(c)), which is rather similar to that observed in the conventional superconductor Nb. For the underdoped samples, however, the SH jump is rather low near T_c, which is much lower than that predicted by the BCS theory. Interestingly, a long tail can be observed far above T_c for the underdoped samples. For these samples, we find that the entropy conservation can’t be achieved at the superconducting transition point (see Fig. 3(c)). One important discovery of this experiment is that the entropy becomes roughly conserved when the long tail part in the normal state is taken into account (see Fig. 3(c)). Considering the successive evolvement of the behavior from underdoped region to overdoped one, we conclude that the Cooper pairs does exist in the temperature region far above T_c for the underdoped samples. In Fig. 4, we present a generic phase diagram derived from our SH data. It is clear that superconductivity related entropy can exist in rather wide region above T_c. This picture deviates from the BCS theory and it may change the understanding to the basic superconducting properties in many aspects. For example, the term ‘‘condensation energy’’ may have a different meaning as compared to a conventional superconductor since the pairing in the normal state certainly contributes a significant part to the total condensation energy. As shown in Fig. 4(d), the normal state contribution to the total condensation energy can be as large as 54% for the underdoped sample with T_c = 11 K. This work gives the evidence that we can’t understand the superconducting condensation in underdoped samples within the BCS scenario from the entropy point of view. Even if the normal state is the so-called small-Fermi-surfaces state, where the superconducting gap can open over again below T_c, it can’t be simply considered as a BCS-type superconducting transition. This work was published in Physical Review Letter 103, 067002(2009) recently.