Due to quantum tunneling, a particle in a double-well potential is not allowed to stay forever in one of the wells. However, it was discovered that when the double-well system is placed under a periodic driving, the particle can be localized in one well when the system parameters are carefully chosen. This phenomenon was called coherent destruction of tunneling (CDT) by Grossmann et al in 1991 (Phys. Rev. Lett. 67, 516 (1991)). It is sometimes also called dynamical localization. CDT has so far generated great interests and has recently been observed experimentally in two very different physical systems.（Phys. Rev. Lett. 98, 263601（2007），Phys. Rev. Lett. 100, 190405（2008））.
　  Since 2005, Prof. Biao Wu from Laboratory of Condensed Matter Theory and Materials Computation of Institute of Physics, Chinese Academy of Sciences, his former PhD student Xiaobing Luo (now associated professor at Jinggangshan University), and former postdoctor Qiongtao Xie (now associated professor at Hunan Normal Univeristy) have conducted a systematic study on the periodically driven Bose-Einstein condensate (BEC) in a double-well potential. Considering the mean-field theory and the interactions between BEC atoms, this system can be regarded as a nonlinear quantum system, different from the single-particle double-well system. To study this system, Wu’s group has developed a new numerical method and obtained for the first time a complete set of Floquet states and quasi-energies for the nonlinear system. They found that there exists a triangular structure in the quasi-energy band, which is unique in nonlinear system. Their further analysis shows that the triangular structure is closely related to the destruction of tunnelling between the two wells. As the triangular structure has a finite width, the destruction of tunnelling occurs accordingly for a finite range of parameters. This is very different from the single-particle system, where CDT occurs at isolated points of parameters. As a result, Wu’s group called it nonlinear coherent destruction of tunnelling (NCDT) (Phys. Rev. A 76, 051802 (R) (2007)).They further proposed that, besides BEC system, nonlinear optical waveguide coupler is an ideal system to observe NCDT.
　  Recently, nonlinear coherent destruction of tunneling was observed experimentally by A.Szameit et al with nonlinear optical waveguide coupler (Optics Letters 34, 2700 (2009)). The experiment by A. Szameit et al confirmed two salient features in the theoretical prediction by Wu’s group: (1) nonlinearity extends the destruction of tunneling to a finite parameter range; (2) periodic driving reduces the threshold power for the tunneling suppression. The coupler used in the experiment is slightly different from the initial proposal: the periodic modulation (or driving) is achieved by modulating the refractive index instead of by bending waveguides as proposed by Wu’s group. In addition, NCDT was partially observed earlier in another experiment (Phys. Rev. Lett.102, 153901 (2009)).
　  Moreover, Wu’s group found that NCDT can be applied to improve the performance of an all-optical switch based on waveguide coupler. This kind of all-optical switch was studied widely in late 1980s (e.g., Appl. Phys. Lett. 51，135 (1987)). The latest development by Wu’s group will likely revive the research along this direction.
　  This research was supported by the NSF of China and the MOST of China.

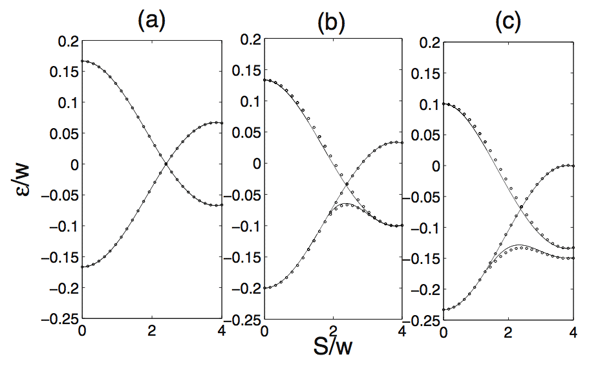Figure 1：The quasi-energy band of a two-mode nonlinear system under periodic driving. (a)c=0;(b)c=0.4;(c)c=0.8.c is the nonlinear parameter. This figure is from Phys. Rev. A 76, 051802 (R) (2007)).

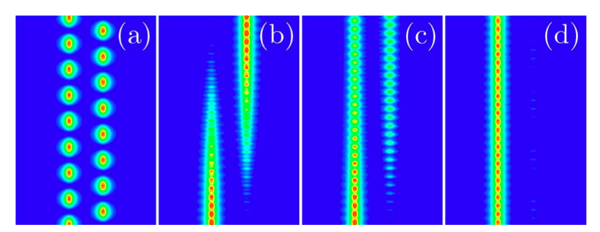Figure 2：Light propagation in a waveguide coupler. (a) without periodic modulation; (b) with periodic modulation and weak laser power; (c) with periodic modulation and strong laser power. This figure is from Opt. Lett. 34, 2700 (2009). References:

［1］ F. Grossmann, T. Dittrich, P. Jung, and P. Hanggi, Phys. Rev. Lett. 67, 516 （1991）.
［2］ G. Della Valle, M. Ornigotti, E. Cianci, V. Foglietti, P. Laporta, and S. Longhi, Phys. Rev. Lett. 98, 263601（2007）.
［3］E. Kierig, U. Schnorrberger, A. Schietinger, J. Tomkovic, and M. K. Oberthaler, Phys. Rev. Lett. 100, 190405（2008）.
［4］Xiaobing Luo, Qiongtao Xie, and Biao Wu, Phys. Rev. A 76, 051802 (R) (2007).
［5］Xiaobing Luo, Qiongtao Xie, and Biao Wu, Phys. Rev. A 77, 053601（2008).
［6］A. Szameit,Y. V. Kartashov,M. Heinrich,F. Dreisow,R. Keil,S. Nolte, A. Tunnermann,V. A. Vysloukh, F. Lederer,and L. Torner， Opt. Lett. 34,2700(2009).
［7］ A. Szameit,Y. V. Kartashov, F. Dreisow,M. Heinrich,T. Pertsch, S. Nolte, A. Tünnermann, V. A. Vysloukh, F. Lederer, and L. Torner，Phys. Rev. Lett.102, 153901 (2009).