Condensed matter systems, including cold atoms in optical lattices, are multi-body systems, but their properties are closely related to the special characteristics of two-body interaction or two-body scattering. In the ultra-cold atomic system, due to the extremely low density of particle numbers, the process of two-body scattering is much more important than that of the many-body scattering, thus becoming more of the focus of attention. Under normal conditions, the range of interaction forces among atoms is very short, so it can be approximately described as the contact potential. The two most important physical parameters are well depth and s-wave scattering length. How to adjust these parameters and study the dependence of the physical nature on them is our greatest concern. The most famous example is the so-called Feshbach resonance, which adjusted the length of s-wave scattering by changing the external magnetic field until the divergence.
Usually, the discussion about the two-body scattering assumes free space, but the cold atom systems are confined in traps with confining potential or periodic lattices. Under these conditions, what changes will happen to the nature of the two-body scattering, can it produce interesting phenomenon similar to the Feshbach resonance? In 1998, Busch et al (Found. Phys. 28, 549 (1998)), after solving the problem of the energy spectrum of two interactive particles with contact potential in harmonic potential, found that the constant of two-body interaction of atoms only depends on the two-body scattering length that can be observed in the experiments, thus making the first contribution to the research of two-body problems in the field of cold atoms. Olshanii (Phys. Rev. Lett. 81, 938 (1998)), while studying the effective scattering of quasi one-dimensional gas (one-dimensional wave guide) that is confined by lateral potential wells, found that by adjusting the strength of confinement potential and making its length proportional to that of the s-wave scattering length, the longitudinal (quasi one-dimensional) interaction will reach a hard-core limit, thus making possible the confinement-induced resonance (known as CIR). They later pointed out (Phys. Rev. Lett. 91, 163201 (2003)) that the mechanism of this resonance is similar to the Feshbach resonance: the states formed by the superposition of excited intrinsic harmonic energy levels at the resonance point in the closed channel happen to have the same energy with the intrinsic ground states in the opened channel. In 2000, Petrov et al (Phys. Rev. Lett. 84, 2551 (2000); Phys. Rev. A 64, 012706 (2001)) studied effective scattering in the quasi two-dimensional system confined by the harmonic potential, and also confirmed the CIR phenomenon. In terms of experiments, the Zurich Group discovered in 2005 the CIR-induced molecular states in the quasi one-dimensional structure in cold atoms (Phys. Rev. Lett. 94, 210401 (2005)), and their experiment results of the confining energy of molecules basically corresponded with the theoretical predictions.
  However, these situations all come under the simplest case in the two-body questions, that is, the degrees of freedom of mass motion and relative motion can be separated. But the interactive (contact potential) parts are only related to the relative positions of the two atoms. Thus, the issue boils down to the question of the single particle with point contact potential moving in the outer field with confining potential and requires only an easy solution. Under normal circumstances, since mass motion and relative motion can not be separated, and the center of mass is excited by the interaction potential, it will be much more difficult to solve the question. In that case, the effective interaction can not be simply described by a scattering length. A typical case in point is the optical lattice system. Although in the past a lot of research focused on the property of interactive atoms in optical lattices, most of them was based on the tight-bounding model and only applies to optical lattices that are relatively deep in the potential wells. So far there has been no systematic research method and uniform understanding about two-body scattering of Bloch wave in optical lattices and molecular states of Bloch waves. Therefore, the study of this question will provide significant guidance to multi-body questions, especially the determination of parameters of the multi-band Hamiltonian, and play an important role in related experimental research, such as dynamics of colliding atoms and quantum information.
  Recently, Prof. Yupeng Wang and Ph.D. Candidate Xiaoling Cui from the Institute of Physics, Chinese Academy of Sciences / Beijing National Laboratory for Condensed Matter Physics (Under prepapration), in collaboration with Professor Fei Zhou from the University of British Columbia in Canada, have made significant progress in low energy effective scattering of the two-body in optical lattices. The idea of this research is based on their preliminary study on high-energy band effects (Phys. Rev. B 79, 180509 (Rapid Communication) (2009) ； Phys. Rev. A 81, 023618 (2010)). By borrowing the idea of phenomenological renormalization and approaching directly from the momentum space down the starting grid, they integrated all the scattering effects of high-energy band into an effective potential of the lowest energy band, and then starting from this effective potential, they further renormalized to obtain the effective scattering of the lowest energy band. This idea originated from the method of renormalization group developed by K. Wilson, who used this method to study the phase transitions, critical phenomena and the Kondo problem, and won the 1982 Nobel Prize in Physics. This approach not only effectively takes into account of the impact of the high energy band effects, but also excludes the defects in dealing with the scattering of two isolated atoms in real space, such as amendments of other atoms to the two-body scattering process, etc., thus facilitating a clearer understanding of the respective contributions of inter-band and scattering within the band to the effective scattering of the low energy band. Their study showed that when the s-wave scattering length of the free space is equal to or greater than the lattice spacing, the imposition of the optical lattices will enable the system to reach a resonance point in a very short time. In this resonance, the inter-band scattering involving high-energy band should play a very important role, similar to CIR in quasi-one dimensional conductivity. In addition, there exists another type of resonance scattering in optical lattices, which can occur in negative scattering length and at arbitrarily small scattering lengths. While the inter-band scattering plays a dominant role in the process, the impact of the effective potential contributed by the inter-band scattering involving high-energy band is very small, thus naturally leading to the commonly used single-band Hubbard model (Figure 1). Studying the energy dependence relationship of the effective scattering matrix, the researchers also found that the limited power range in optical lattices will induce the extremely rich curves different from those in the free-space. (Figure 2). Finally, with the help of experimental measurements, they studied the momentum distribution of the Bloch molecular states induced by resonance, and discussed, referring to electron-cavity symmetry, the symmetrical mapping between this molecule at the ground state and another highly excited molecular state induced by the exclusion that has been observed experimentally (Nature (London) 441, 853 (2006)) (Figure 3). The significance of this work lies in its proposition of a new method (phenomenological renormalization) to accurately study the two- body scattering problems of the system of the inseparable and variable cold atoms, thus holding universal significance to the study of multi-body scattering effects in cold atom system. This study has received great attention and recognition from international scholars of this particular field, and has been published in the April 2010 issue of Phys. Rev. Lett., 104,153201 (2010)). This study was jointly supported by the Chinese Academy of Sciences, the National Natural Science Foundation of China and the 973 Project, and Institute of Higher Learning of the Natural Sciences and Engineering Research Council of Canada.

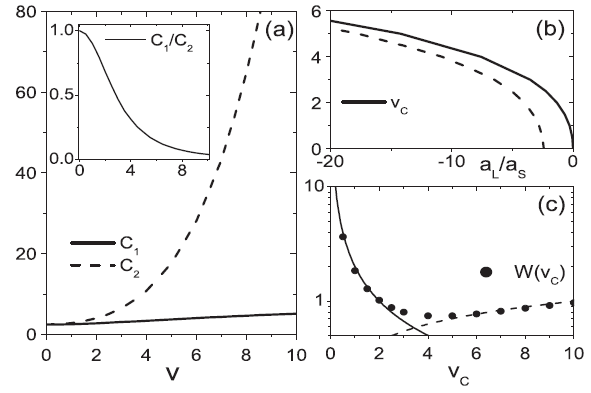Figure 1. Resonance scattering of two-body zero-effective energy in optical lattices

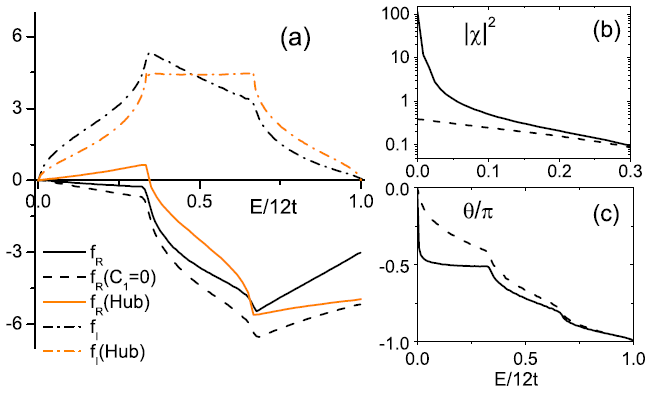Figure 2. Dependence of two-body scattering matrix on energy E in optical lattices, and sectional area and phase shift of low energy scattering

Figure 3. Momentum distribution in real space of the two-body confining states induced by resonance