The topological insulator is a novel state of matter where the bulk is insulating but the surface is conducting which is robust due to topological protection. In general, the topological insulators are believed to appear in two- and three-dimensional systems, an interesting question is whether topological insulator can be realized in the one-dimensional (1D) system too?
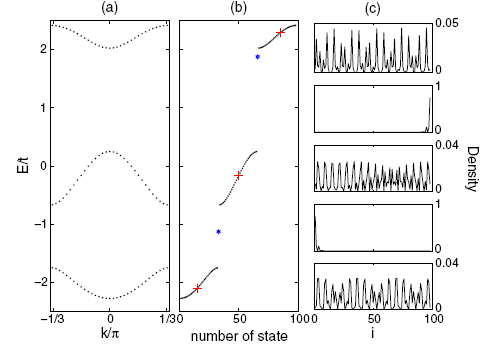
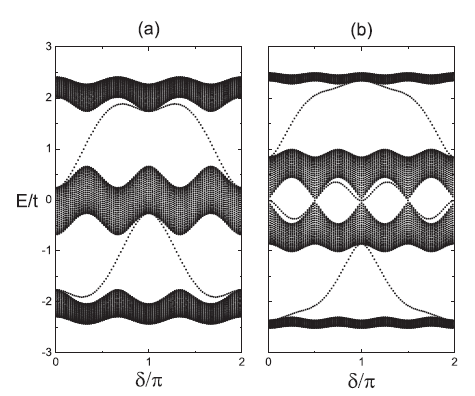
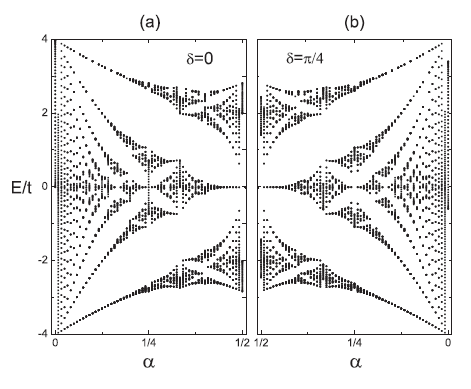
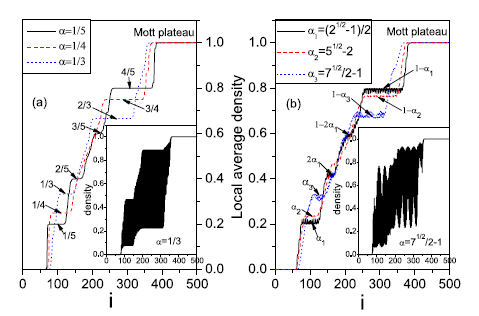
　  Recently, Prof. Shu Chen and his Ph.D. student Li-Jun Lang and postdoctor Xiaoming Cai at the Beijing National Laboratory for Condensed Matter Physics, the Institute of Physics, Chinese Academy of Sciences (IOP, CAS), have made progress in the study of the topological properties of the 1D optical superlattice system.  They show that one-dimensional quasiperiodic optical lattice systems can exhibit edge states and topological phases which are generally believed to appear in two-dimensional systems. When the Fermi energy lies in gaps, the Fermi system on the optical superlattice is a topological insulator characterized by a nonzero topological invariant. The topological nature can be revealed by observing the density profile of a trapped fermion system, which displays plateaus with their positions uniquely determined by the ration of wavelengths of the bichromatic optical lattice. The butterflylike spectrum of the superlattice system can be also determined from the finite-temperature density profiles of the trapped fermion system. This finding opens an alternative avenue to study the topological phases and Hofstadterlike spectrum in one-dimensional optical lattices.

　  The related work is published in Phys. Rev. Lett. 108, 220401 (2012) and supported by the NSF of China and MOST.

Related reference:
Edge States and Topological Phases in One-Dimensional Optical Superlattices,
L.-J. Lang, X. M. Cai, and S. Chen, Phys. Rev. Lett. 108, 220401 (2012)
Full article can be found at: 10.1103/PhysRevLett.108.220401

Fig1：Energy spectrum and states of 1D optical superlattice with period theree.。(a) is the band structure for periodic system，(b) is the energy spectrum for open-boundary system，There appears the edge state in the gap regime. (c) shows the extended states and localized edge states. （Image by Shu Chen et al.）

Fig2：Energy spectrum for open-boundary superlattice system versus the phas.  (a) for period-3 system，(b) for period-4 system。（Image by Shu Chen et al.）

Fig3：The butterfly spectrum of the 1D superlattice system. （Image by Shu Chen et al.）

Fig4：The density distribution of the Fermi superlattice system in a harmonic trap. The position of the plateau is completely determined by the ration of wavelengths of the bichromatic optical lattice, from which one can determine the topological Chern number of the filled-band system. （Image by Shu Chen et al.）