Recently, a research group led by Prof. LIU Wuming in the Institute of Physics, Chinese Academy of Sciences has demonstrated that Goldstone and Higgs modes can be observed in optical systems with only a few (artificial) atoms inside a cavity. They establish this connection by studying the U(1)/Z₂ Dicke model where N qubits (atoms) coupled to a single photon mode.

It was well known that a broken global continuous symmetry in quantum phases leads to two associated collective modes: the massless Goldstone mode and a massive Anderson-Higgs amplitude mode (for topological ordered phases, see). The Goldstone modes have been detected in a quantum anti-ferromagnet a superfluid and also in cold atom systems. However, the massive Higgs mode is much more difficult to detect in experiments. Even so, the Higgs amplitude mode was detected by Raman scattering in superconductors and by in-elastic neutron scattering in a quantum anti-ferromagnet near its quantum phase transition to a valence bond solid. Unfortunately, due to the Galilean invariance, the phase mode and amplitude mode are conjugate variables, the conjugate pair only leads to a Goldstone mode. There is no Higgs mode inside a superfluid. There was a report that the Higgs amplitude mode was detected in a three dimensional superfluid of strongly interacting bosons in an optical lattice by Bragg spectroscopy. Most recently, the Higgs amplitude mode and its decay rate were detected in cold atoms loaded in two dimensional optical lattice near the superfluid to Mott transition by slightly modulating the lattice depth within a linear response regime. Notably, the experiment detected discrete natures of the Higgs modes in a trapped system. In a relativistic quantum field theory, it is the well known Higgs mechanism which generates various mass spectrum of elementary particles. Although the various elementary particles have been discovered with the predicted masses, the original massive Higgs particle stays elusive until it was finally discovered with its mass,125GeVand width,6MeVin the recent LHC experiments

Researchers from Prof. LIU Wuming’s group determine the Goldstone and Higgs modes inside the super-radiant phase and their corresponding spectral weights by performing both 1/J=2/N expansion and exact diagonalization (ED) study at a finite N. They find nearly perfect agreements between the results achieved by the two approaches when N gets down even to N=2. The quantum finite size effects at a few qubits make the two modes quite robust against a small counter-rotating wave term. They present a few schemes to reduce the critical coupling strength, so the two modes can be observed in several current available experimental systems by just conventional optical measurements.

This work was supported by National Natural Science Foundation of China  ,  the National Key Basic Research Special Foundation of China，and Beijing Municipal Commission of Education.

The work was published on Scientific Reports 3, 3476 (2013).
http://www.nature.com/srep/2013/131211/srep03476/full/srep03476.html

CONTACT:
Prof. LIU WuMing
Institute of Physics
Chinese Academy of Sciences
Email: wmliu@iphy.ac.cn

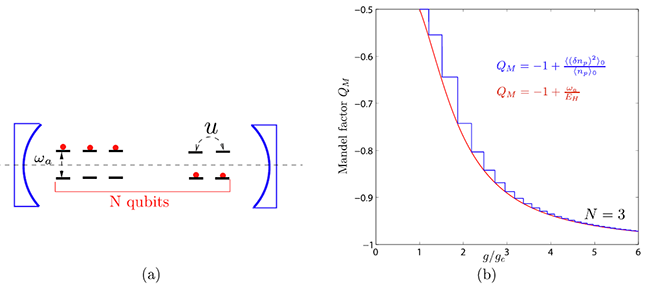Figure 1| (a) N (artificial) atoms are placed on anti-nodes of a cavity. u is the repulsive qubit-qubit interaction which can be tuned to reduce the critical coupling gc.ωa is the cavity photon frequency. (b) The analytical Mandel factor QM (red) against the ED result (blue) at N=3. It is a number squeezed state inside the superradiant phase. (Image by Prof. LIU’s group)

Figure 2| The ED results (See the Methods section) of the energy levels E measured by subtracting the ground-state energy versus g/gc at resonance ωa=ωb with N=5 atoms. Different colors of the energy curves correspond to several smallest numbers of total excitations number P=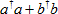. The dashed vertical lines correspond to the critical values of g where the number of total excitations P in the ground state increases by one. ωbis the cavity photon frequency. (Image by Prof. LIU’s group)

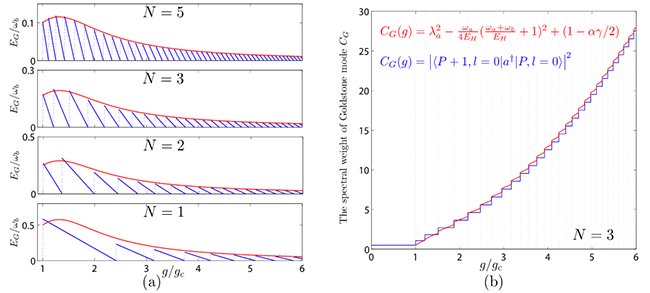Figure 3| (a) The analytical Goldstone mode at α=-1/2 , EG=(α=-1/2)=D(g)=(red line) are contrasted with the ED result EG=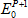-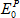(blue lines) at N=5, 3, 2, 1 respectively. It is remarkable that the analytical result can even map out broad peaks at small P in the ED results very precisely. (b) The analytical spectral weight (red) of the Goldstone mode CG against the ED result (blue) at N= 3. D is the phase diffusion constant. (Image by Prof. LIU’s group)

Figure 4| (a) The analytical relation E0=EH+EG（EH in red line) is satisfied by the ED optical mode E0=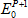-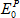(blue lines) at N=3 except at the first few steps. (b) The analytical spectral weight (red) of the optical mode Co against the ED result (blue) at N=3. (Image by Prof. LIU’s group)

Figure 5| (a) The analytical Higgs energy EH(red) against the ED result EH=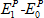(blue) at N=3. (b) The analytical spectral spectral weight CH(red) for the Higgs mode against the ED result (blue) at N=3. (Image by Prof. LIU’s group)