Monte Carlo study reveals the parent state of quantum phases
Date:20-05-2019 Print
Numerical simulations provide the first concrete evidence of 2D (U1) deconfined matter, an exotic phase whose existence has been pursued by both condensed-matter and high-energy physicists.
An international research team, led by Prof. Zi Yang Meng from the Institute of Physics, Chinese Academy of Sciences, comprised of Dr. Xiao Yan Xu from Hong Kong University of Science and Technology, Associate Prof. Yang Qi from Fudan University, Assistant Prof. Long Zhang from Kavil Institute of Theoretical Sciences, Chinese Academy of Sciences, Prof. Cenke Xu from University of California, Santa Barbara and Prof. Fakher Assaad from University of Wuerzburg, have made a substantial discovery in novel state of quantum matter via large-scale Monte Carlo simulations and field theoretical analysis. The research work is published in the latest issue of Physical Review X [1]. Below is a brief description of their story:
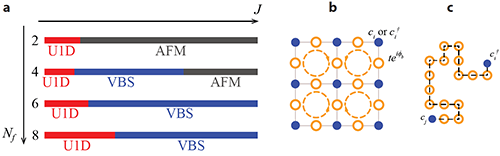
Fig.1. a. Phase diagram spanned by the Fermi flavors Nf and the strength of gauge field fluctuations J of the model shown in b. U1D stands for the U(1) deconfined phase where the fermions dynamically form a Dirac system. This phase corresponds to the algebraic spin liquid where all correlation functions show slow power-law decay. VBS stands for valence-bond-solid phase and AFM stands for the antiferromagnetic long-range ordered phase (Neel phase). b. Sketch of the model, the yellow circles represent the gauge field attached to each fermion hopping, and the yellow dashed lines stand for the flux term per plaquette. c. The gauge invariant propagator for fermions with a string of gauge fields attached.
According to the new paradigms in quantum material science, for some magnets and compounds, the elementary excitations are no longer the constituent particles such as electrons and ions that comprised of the material, instead, they are so-called spinons whose mutual interactions are mediated by the emergent gauge fields. Those spinons come from the fractionlization of spins (e.g. one spin is fractionalized into two spinons). Such quantum state of matter are dubbed quantum spin liquid and depends on the symmetry structure of the gauge field, the spin liquid can be of Z_2 or U(1) type, etc. In the latter case, the spinon and U(1) gauge field, put on a 2D square lattice, would form very unique situation where the spinons could have linear dispersion (U(1) algebraic Dirac spin liquid, Dirac comes from the linear dispersion and algebraic means the spinons are gapless hence they are bestowed with algebraic decay correlation functions) and at the same time they are strongly interacting among each other with the help of U(1) gauge field fluctuations. The schematic description of the lattice model and spinon Green’s function are shown in Fig. 1 (b) and (c), and the obtained phase diagram is shown in Fig. 1 (a). To condensed matter physicists, the existence of 2D U(1) algebraic spin liquid is important as it is proposed to explain the perplexing experimental observations of many frustrated magnets and high-temperature superconductors.
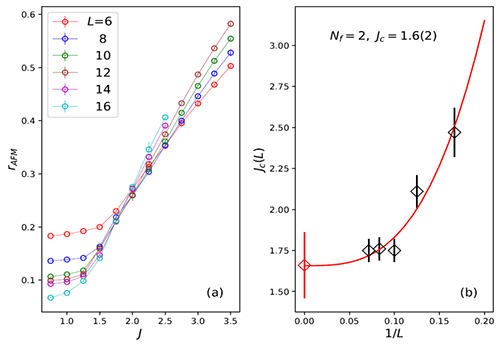
Fig.2. (a) The antiferromagnetic correlation ratio through the U1D-to-AFM transition at Nf=2. The crossing points are the transition points separating the U(1) deconfined phase and the AFM confined phase. (b) The extrapolation of the crossings estimates the U1D-to-AFM transition point Jc=1.6(2) for Nf=2.
It turns out that such as a quantum state of matter -- the U(1) algebraic spin liquid to condensed matter physicist -- is also what high energy physicists are dreaming for years, in their language, it is the deconfined state of matter in quantum electrodynamics. The U(1) gauge fields describing electromagnetic interaction mediates the interaction between the deconfined -- that is, loosely speaking, fractionalized or splitted from a convention particle or field -- fermionic matter fields (think about deconfinement of quark) with different flavors N_f. High energy physicists has proved that the pure U(1) gauge field in space-time dimension 2+1, would always be confined, but whether by adding fermionic matter fields would change the situation is an important question to them. In short, from both condensed matter and high energy communities, the existence of 2D U(1) algebraic spin liquid or the U(1) deconfined matter, is of high interests and scientific value, the only question is, DOES it really exist?
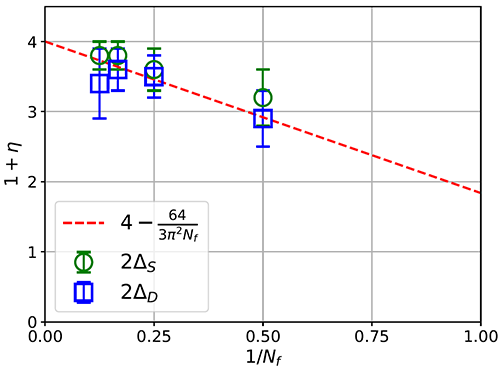
Fig.3. Dimension of spin (gren circles) and dimer (blue squares) in the U1D phase as a function of Nf. The dashed red line corresponds to the 1/Nf perturbative calculation, 1+eta = 4-[64/(3pi^2 Nf)], taken from Ref. [2]. Note here Nf corresponds to the number of four-component Dirac fermions.
In this recent PRX paper, Xu et al. designed a lattice model by discretizing U(1) gauge fields into a space-time lattice (so called lattice gauge theory) interacting with fermions. They simulated the model non-perturbatively with quantum Monte Carlo method, on two of the world largest supercomputers (Tianhe-1A and Tianhe-2 in the National Supercomputer Centers in Tianjin and Guangzhou, respectively), and for the first time provided concrete evidence of the existence of 2D U(1) deconfined matter.
They considered fermion species N_f = 2,4,6 and 8 and observed U(1) algebraic spin liquid phases at all cases where spin and dimer operators share the same scaling dimension, a smoking-gun signature of such exotic state of matter. The obtained phase diagram is shown in Fig.1 (a), the example of the determination of the phase transition between U1D phase and AFM phase at the case of Nf=2 is shown in Fig.2, and the scaling dimensions of spin-spin and dimer-dimer correlation functions inside the U1D phase, as a function of the Nf, is shown in Fig.3 and the results shows consistent behavior when Nf becomes large with the 1/Nf limit results as obtained in Ref.[2].
They also observed continuous deconfinement to confinement transitions when tuning coupling constant in model. Apart from these, they have also found at N_f=4 a very interesting new type of quantum critical point, beyond their previous discovery (see popular summary in Ref. [3]). Overall, the richness of the phase diagram and firm existence of the U(1) deconfined state of matter will certainly trigger a number of future investigations on the numerical and analytical fronts, both in the condensed matter and in the high energy communities.
Acknowledgement
The large-scale simulations are performed on the Tianhe-1A platform at the National Supercomputer Center in Tianjin and Tianhe-2 platform at the National Supercomputer Center in Guangzhou, the authors acknowledge the technical support and generous allocation of CPU time from these centers. The authors also thank the funding support from the Ministry of Science and Technology of China through the National Key Research and Development Program (2016YFA0300502, 2018YFA0305802), the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB28000000, XDPB08-4, XDB28040200), the National Science Foundation of China (11574359, 11674370), the HKRGC through HKUST3/CRF/13G and C6026-16W and the DFG research unit FOR1807.
Journal Reference
[1] Monte Carlo Study of Lattice Compact Quantum Electrodynamics with Fermionic Matter: The Parent State of Quantum Phases,
Xiao Yan Xu, Yang Qi, Long Zhang, Fakher F. Assaad, Cenke Xu, and Zi Yang Meng,
Phys. Rev. X 9, 021022 (2019)
https://journals.aps.org/prx/abstract/10.1103/PhysRevX.9.021022
[2] Spin Correlations in the Algebraic Spin Liquid: Implications for High-Tc Superconductors,
W. Rantner and X.-G. Wen,
Phys. Rev. B 66, 144501 (2002).
[3] Duality between the Deconfined Quantum-Critical Point and the Bosonic Topological Transition,
Yan Qi Qin, Yuan-Yao He, Yi-Zhuang You, Zhong-Yi Lu, Arnab Sen, Anders W. Sandvik, Cenke Xu, and Zi Yang Meng,
Phys. Rev. X 7, 031052(2017)


