Twisted bilayer graphene at charge neutrality
Date:21-10-2019 Print
Just one year after researchers at MIT stunned the physics world with the discovery of the magic-angle for stacked sheets of graphene [1,2], many advances in theoretical and experimental studies in the twisted graphene heterostructures have been achieved, from twisted bilayer graphene to trilayer graphene [3] and twisted double bilayer graphene [4,5]. At the model level, it is clear that fully controlled calculation of the microscopic graphene heterostructure with many-body effect taking into account is almost impossible, due to the large number of atoms in an unit cell of Moire superlattice. It is the effective models, constructed from the Wannier orbitals and implemented on the emergent honeycomb lattice, for example the model by Mikito Koshino, et al [6], offer the possibility for tight-binding type of description of the systems with effective but limited number of degrees of freedom, and allow people to analyze and understand the rich phenomena of correlated insulators, superconductivity, strange metal, etc, associated with interaction effects on the flat bands.
Nevertheless, the field of magic-angle twisted graphene is so young that many basic questions are yet to be answered, for instance, not only the pairing symmetry of the superconductivity phases are far from understood, people also do not understand the very nature of the correlated insulator phases, i.e., whether they are of charge, spin, valley or other types of order. This is partially due to the fact that the aforementioned effective models of the flat bands are still not fully constructed with consensus, and also partially because the cluster charge interaction present in the system is too hard to handle in an controlled manner.
Recently, an first attempt made by Mr. Yuanda Liao and Prof. Zi Yang Meng from Institute of Physics, Chinese Academy of Sciences and Dr. Xiao Yan Xu from University of Science and Technology of Hong Kong and University of California at San Diego, in trying to answer above questions with unbiased large-scale numerical method taking the full quantum many-body effect into account, has been put forward and achieved interesting results [7]. They discovered that one of the existing four bands model [6] (two orbital and two valley) is free from the minus-sign-problem when considering the cluster charge interaction at the neutrality of carrier density, and consequently performed detailed numerical investigation of the ground state phase diagram of the model.
Their efforts revealed that the Fermi velocity of the Dirac fermions is renormalized as the cluster charge interaction increases, until a mass term emerges and a quantum critical point of 3D N = 4 Gross-Neveu chiral XY universality with emergent continuous symmetry separating Dirac semi-metal (DSM) phase to plaquette valence bond solid (pVBS) insulator is established. Further enhancement of the interaction drives the system into a columnar valence bond solid (cVBS) phase, the transition between pVBS and cVBS phase is first order but of topological nature.
This work [7] points out the direction of employing exact numerical methodologies to investigate the twisted graphene heterostructure models, and put the speculations that the experimentally observed phenomena in the twisted graphene layers have relevance with possible quantum critical fluctuations into solid footing.
This work titled "Valence Bond Orders at Charge Neutrality in a Possible Two-Orbital Extended Hubbard Model for Twisted Bilayer Graphene" is published in the latest issue of Phys. Rev. Lett. 123, 157601(2019).
 |
| FIG. 1. Ground state phase diagram of the two-rrbital extended Hubbard Model for twisted bilayer graphene, revealed from quantum Monte Carlo simulation in Ref.[7]. |
 |
| FIG. 2. (a) The bond-bond correlation ratio RB and the DSM-to-pVBS transition happens at the crossing point of the data of Uc/t=25.1(2). (b) data collapse analysis of the structure factor CB(K) with 3D N = 4 Gross-Neveu chiral XY exponents. |
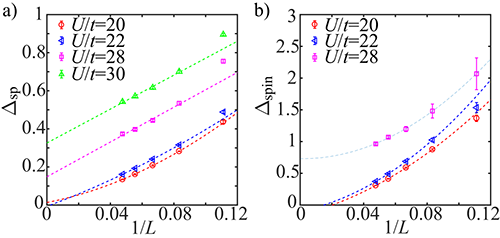 |
| FIG.3. (a) The 1/L extrapolation of the single-particle gap, the gap opens (the metal-insulator DSM-to-pVBS transition) between U/t= 22 and U/t =28, consistent with the Uc/t obtained from the bond correlation ratio in Fig. 2(a). (b) The 1/L extrapolation of spin gap, the spin gap opens hand in hand with the single-particle gap as the establishment of pVBS order. |
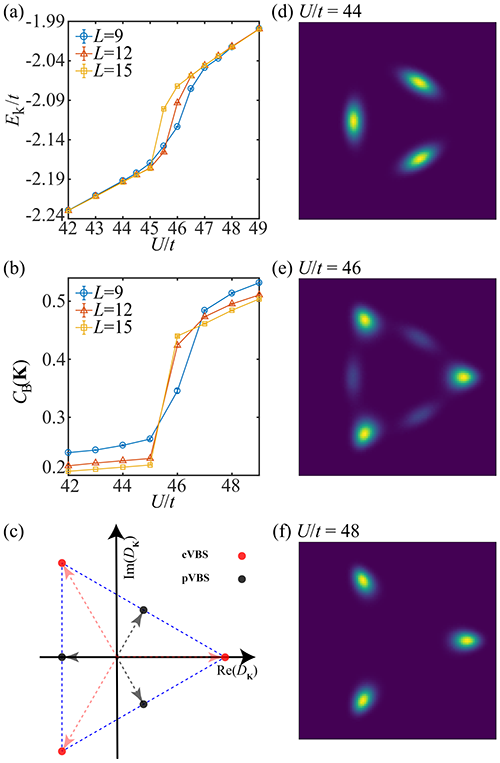 |
| FIG.4. The first order phase transition between pVBS to cVBS at U/t~45, the histograms reveal the different internal structure of the two VBS insulators. |
Acknowledgement:
The large-scale simulations are performed on the Tianhe-1A platform at the National Supercomputer Center in Tianjin and Tianhe-2 platform at the National Supercomputer Center in Guangzhou, the authors acknowledge the technical support and generous allocation of CPU time from these centers. The authors also thank the funding support from the Ministry of Science and Technology of China through the National Key Research and Development Program (2016YFA0300502), the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB28000000), the National Science Foundation of China (11574359) and Research Grants Council of Hong Kong Special Administrative Region of China through Grants 17303019 and C6026-16W and the DFG research unit FOR1807 and Mercator Fellow.
Reference:
[1] Y. Cao, V. Fatemi, A. Demir, S. Fang, S. L. Tomarken, J. Y. Luo, J. D. Sanchez-Yamagishi, K. Watanabe, T. Taniguchi, E. Kaxiras, R. C. Ashoori, and P. Jarillo-Herrero, Nature (London) 556, 80 (2018).
[2] Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras, and P. Jarillo-Herrero, Nature (London) 556, 43 (2018).
[3] Guorui Chen, Aaron L. Sharpe, Patrick Gallagher, Ilan T. Rosen, Eli J. Fox, Lili Jiang, Bosai Lyu, Hongyuan Li, Kenji Watanabe, Takashi Taniguchi, Jeil Jung, Zhiwen Shi, David Goldhaber-Gordon, Yuanbo Zhang, Feng Wang, Nature 572, 215-219 (2019).
[4] Cheng Shen, Na Li, Shuopei Wang, Yanchong Zhao, Jian Tang, Jieying Liu, Jinpeng Tian, Yanbang Chu, Kenji Watanabe, Takashi Taniguchi, Rong Yang, Zi Yang Meng, Dongxia Shi, Guangyu Zhang, arXiv:1903.06952 (2019).
[5] Xiaomeng Liu, Zeyu Hao, Eslam Khalaf, Jong Yeon Lee, Kenji Watanabe, Takashi Taniguchi, Ashvin Vishwanath, Philip Kim, arXiv:1903.08130 (2019).
[6] M. Koshino, N. F. Q. Yuan, T. Koretsune, M. Ochi, K. Kuroki, and L. Fu, Phys. Rev. X 8, 031087 (2018).
[7] Yuan Da Liao, Zi Yang Meng, Xiao Yan Xu,
Phys. Rev. Lett. 123, 157601 (2019).


