Higher-order topology and monopole nodal lines in Transition Metal Dichalcogenides XTe2 (X = Mo, W)
Date:18-11-2019 Print
In recent years, transition metal dichalcogenides (TMDs) have garnered great interest as topological materials [1,2]. In particular, monolayers of centrosymmetric β-phase TMDs have been identified as 2D topological insulators (TIs), and bulk crystals of noncentrosymmetric γ-phase MoTe2 and WTe2 have been identified as type-II Weyl semimetals. However, angle-resolved photoemission spectroscopy and STM probes of these semimetals have revealed huge, arc-like surface states that overwhelm, and are sometimes mistaken for, the much smaller topological surface Fermi arcs of bulk type-II Weyl points.
In this Letter, we calculate the bulk and surface electronic structure of both β- and γ-MoTe2. We find that β-MoTe2 is, in fact, a Z4-nontrivial higher-order TI (HOTI) [3,4] driven by double band inversion and exhibits the same surface features as γ-MoTe2 and γ-WTe2 [Fig. 1]. We discover that these surface states are not topologically trivial, as previously characterized by the research that differentiated them from the Weyl Fermi arcs but, rather, are the characteristic split and gapped fourfold Dirac surface states of a HOTI.
In β-MoTe2, the HOTI phase indicates that it would exhibit helical pairs of hinge states if it were bulk insulating, and in γ-MoTe2 and γ-WTe2, these surface states represent vestiges of HOTI phases without inversion symmetry that are nearby in parameter space [Fig. 2]. Using nested Wilson loops and first-principles calculations, we explicitly demonstrate that, when the Weyl points in γ-MoTe2 are annihilated, which may be accomplished by symmetry-preserving strain or lattice distortion, γ-MoTe2 becomes a nonsymmetry-indicated, noncentrosymmetric HOTI.
We also show that, when the effects of spin-orbit coupling are neglected, β-MoTe2 is a nodal-line semimetal with Z2-nontrivial monopole nodal lines (MNLSM). This finding confirms that MNLSMs driven by double band inversion are the weak-spin-orbit coupling limit of HOTIs, implying that MNLSMs are higher-order topological semimetals with flat-band-like hinge states, which we find to originate from the corner modes of 2D “fragile” TIs.
This work [5] was supported by the National Natural Science Foundation of China (Grants No. 11504117 and No. 11774317).
References:
[1] Barry Bradlyn et al., "Topological quantum chemistry", Nature, 547 (2017).
[2] Vergniory, M.G., et al., “A complete catalogue of high-quality topological materials”, Nature, 566, 480-485 (2019).
[3] Po, H. C. et al., "Symmetry-based indicators of band topology in the 230 space groups", Nat. Comm. 8, 50 (2017).
[4] Z. Song et al., "Quantitative mappings between symmetry and topology in solids", Nat. Comm. 9, 3530 (2018).
[5] Zhijun Wang et al., Phys. Rev. Lett. 123, 186401 (2019).
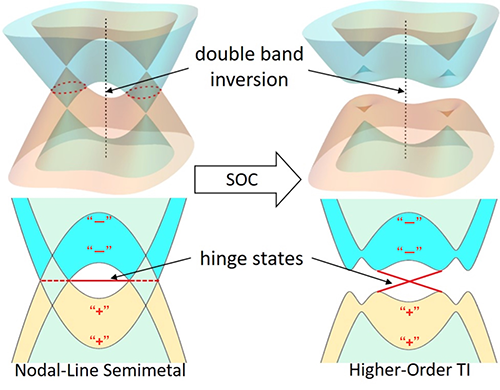
FIG. 1. When two pairs of degenerate bands with positive parity eigenvalues and two pairs with negative parity eigenvalues are inverted at a TRIM point, the occupied bands cannot be expressed as a linear combination of EBRs and the Z4 topological index is changed by 2. In a T -symmetric crystal with vanishing SOC, this process may nucleate a pair of Dirac nodal lines with nontrivial monopole charge (MNLs) (dashed lines in left panel). On the 1D hinges, the projections of the MNLs are spanned by nearly flat bands. These hinge states represent an example of higher-order topology in a bulk- gapless system: they are the (d-2)-dimensional generalization of drumhead surface states, and are the spinless analogs of the hinge states recently predicted in spinful Dirac SMs. When I-symmetric SOC is introduced, the MNLSM will necessarily gap into a HOTI if all other bands are uninverted, and the flat-band hinge states will open into helical pairs spanning the bulk and surface gaps. HOTIs driven by this “double band inversion” (DBI) as shown in this Letter, β-MoTe2.
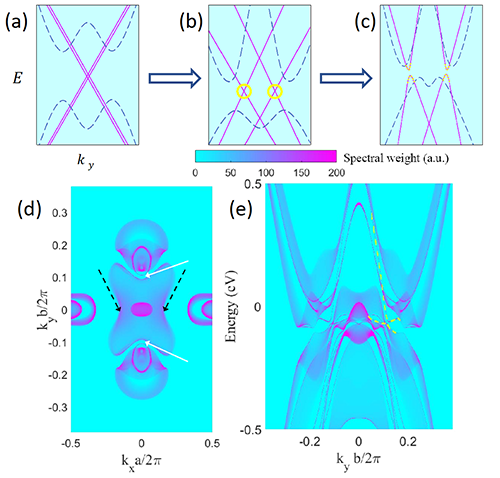
FIG. 4. (a)-(c) Schematic surface state evolution of a HOTI driven by DBI. (d) Spectral weight at EF of states on the (001) surface of β-MoTe2 plotted as a function of kx,y and (e) along kx=0 as a function of energy.
Contact:
Institute of Physics
Zhijun Wang
Email:wzj@iphy.ac.cn
Key word:
Monopole nodal lines, Higher-order topological insulators, Transition Metal Diachalcogenides
Abstract:
Higher-order topology and monopole nodal lines are revealed in Transition Metal Dichalcogenides XTe2 (X = Mo, W)


