Precision lock-in frequency meters developed
Date:20-07-2020 Print
Phase is a fundamental concept widely accepted in physics and informalogy, which has been used as an important indicator of the overall state evolution for many-body system. Therefore, famous physicist Chen-Ning Yang has attributed phase as one of the three main themes of development in physics in the 20th century, together with symmetry and quantum. Phase-locking technology originated from the invention of "coherent communication" in 1932, and later became an important "phase-locked loop" method for maintaining synchronization, which worked in time dimension without function of amplitude detection. Expanding from the time dimension to the signal strength dimension, based on phase-sensitive detection, the higher frequency alternating amplitude signal is down-converted to a lower frequency signal. As a result, with the ability of suppressing noise, lock-in amplifiers is usually indispensable in weak signal measurement. The lock-in amplifiers are essentially an ultra-narrowband filter with unique advantage to extract the amplitude and phase of the AC signal buried in the noise even if it is faint to nanovolts. It has extremely high frequency domain resolution and has been widely used for a long time. Industrial enterprises and scientific research fields such as physical property measurement, scanning probe microscope, laser spectroscopy, non-destructive testing, spectrum-based medical imaging, seismic measurement, etc. Lock-in amplifiers can also be found in emerging industry application scenarios, such as quantum computers, precision IoT sensing, high-precision component grading testing, third-generation biological gene sequencing, space gravitational wave detection, etc. To a certain extent, the level of application of the lock-in amplifier as a precision measurement tool for the underlying signal reflects the scientific research capability and industrialization level.
In the research on the basic principle of phase-locking, Dr. LU Jun from Institute of Physics, Chinese Academy of Sciences noticed that the measurement result of the traditional method is a complex number corresponding to the frequency of the reference signal. The real alternating frequency of the measured complex number is used as a hidden variable, which is usually regarded as exactly the same as the reference frequency. The frequency of the measured signal and the frequency of the reference signal will deviate during the transmission channel or system strain process. Some signals such as passively observed signals cannot be controlled in advance. The inconsistency between the preset frequency and the real frequency will eventually lead to inaccurate phase difference and amplitude measurement. The idea to solve this problem is actually discarding the assumption that the frequency of the measured signal is consistent with the frequency of the fixed reference signal. After improving the frequency functional analysis through the phase-locked algorithm, the researcher has simultaneously solved the anti-noise frequency measurement and accurate phase lock of the measured signal. The new developed method is hence called lock-in amplifier with frequency measurement or lock-in frequency meter (LIF). After theoretically deducing the local function form of the phase-locked spectrum of the single-period signal near the estimated frequency point, and using three-point fitting for frequency measurement, the new method can avoid the deviation problem of the parabolic function. As a result, the accuracy reaches the limit of statistical theory, and the efficiency has been greatly enhanced. Based on simulation result, the complexity of the algorithm has reduced from O(N*logN) of the fast Fourier transform FFT to O(N) dependence. In addition to the theoretical lower limit Cramers-Raw Lower Bound, the researcher found the measurement uncertainty of the phase-lock frequency meter also has an upper limit Lock-in Upper Bound due to the limited sampling window. Therefore, the new method quantitatively gives the relationship formula of the theoretical lowest measurable signal-to-noise ratio for lock-in amplifiers.
The new method simultaneously solves the problems that the usual frequency meter cannot measure low signal-to-noise ratio signals and the phase-locked reference frequency must be preset. Because the preset parameters are reduced, it is easy to increase the intelligence of the lock-in amplifier and possess the potential to be embedded in a multimeter. After designing the new phase-locking algorithm for frequency measurement, LU Jun realized a cross-platform solution from circuit design, FPGA programming, ARM embedded and host computer programs through the collaborative enterprise Yanchuangda, and finally integrated analog and digital circuit technology to form a new domestically-made phase lock prototype. The noise floor measured by the new phase lock at 1 kHz frequency point with 1 second integration time is 1nV/√Hz; the frequency measurement accuracy can reach 1 ppb (one-billionth) at 10 kHz. Through the system test of signal and different types of noise premixing and extraction, the results show that the frequency measurement accuracy under noise is close to the theoretical limit.
This study entitled “Lock-in frequency measurement with high precision and efficiency” was published on Review of Scientific Instruments.
This work is under supports from National Natural Science Foundation of China (No. 51327806 and 61575209), Fujian Institute of Innovation (Grant No. FJCXY18040302) and Youth Innovation Promotion Association of Chinese Academy of Sciences (No.2018009 and No.2018024).
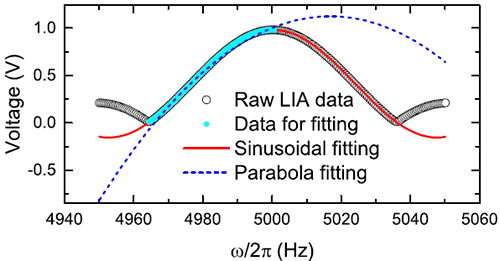
Fig. 1 Principle of the LIF approach. (Image by Institute of Physics)
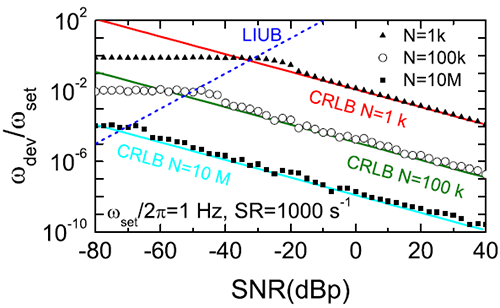
Fig. 2 Comparison of the simulated LIF precision with the theoretical Cramer–Rao lower bound and lock-in upper bound.. (Image by Institute of Physics)
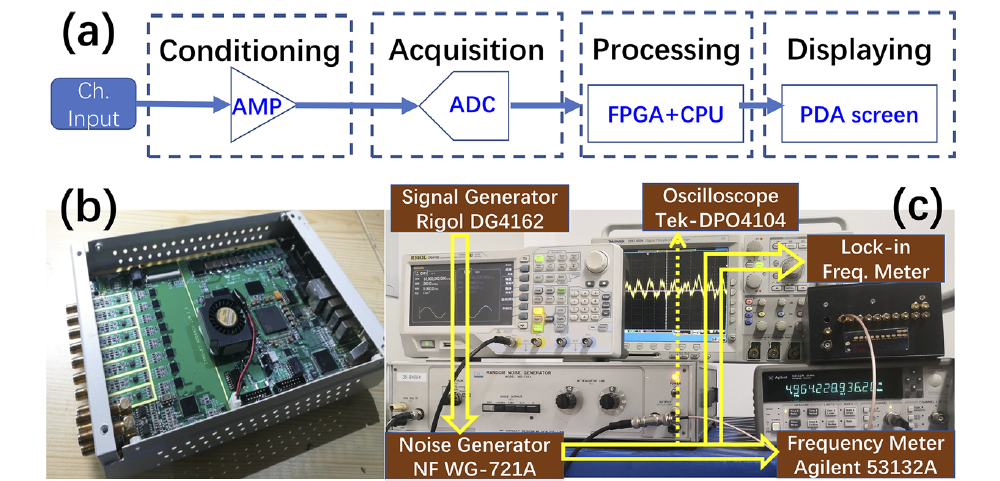
Fig. 3 (a) Implementation structure and (b) circuit-board of the LIF device. (c) Testing platform with a signal generator, a noise generator, and a standard frequency meter as well as the LIF instrument, where an oscilloscope is used for recording raw waveforms. (Image by Institute of Physics)
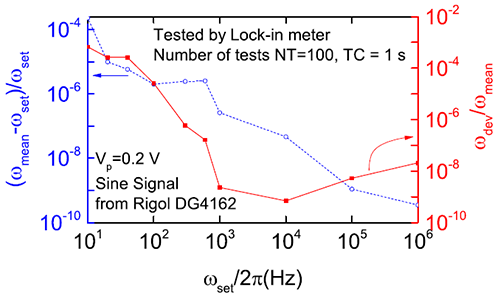
Fig. 4 Frequency-dependent LIF measurement results. (Image by Institute of Physics)
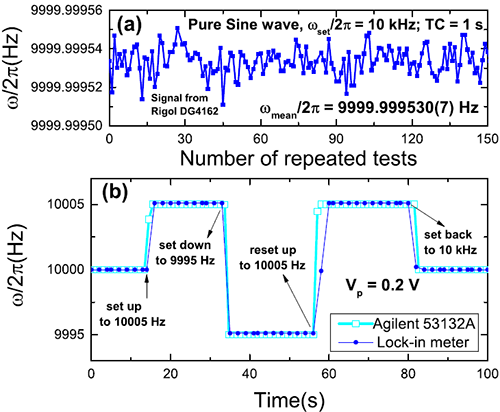
Fig. 5 (a) Repeated LIF test results for pure sine signals at 10 kHz and (b) a comparison of response time tests to the results of a standard frequency meter. (Image by Institute of Physics)
Contact:
Institute of Physics
LU Jun
Email:lujun@iphy.ac.cn
Key word:
Frequency spectrum; Frequency measurement; Cramer-Rao lower bound; Phase lock loop;
Abstract:
This paper describes a new method of frequency measurement based on lock-in amplifiers (LIAs). In contrast to other frequency measurement methods, such as fast Fourier transformation (FFT), zero crossing, and scanning autocorrelation, this method is based on an adaptable LIA design for high-precision determination of not only the frequency but also the amplitude and phase of periodic signals, even when they are buried in heavy noise with low signal-to-noise ratios. Mathematical derivation of the local spectrum around the center frequency is performed, and the local frequency spectrum waveform of the sinusoidal signal, regardless of whether it is pure or noisy, is found to be exactly of a bell shape that can be described by a three-parameter sine function. Based on the principle of LIAs, the correct frequency can produce a peak amplitude in the local spectrum. As a result, the amplitudes of three frequency points around the target frequency can be used to precisely determine the peak frequency via sinusoidal fitting. The efficiency of the proposed method is log2(N) times that of FFT. Simulation results show that the new algorithm can reach the theoretical Cramer–Rao lower bound and remain below a lock-in upper bound. The new frequency measurement method has been implemented in an field-programmable gate array (FPGA)-based device and systematically tested for its dependence on the frequency, amplitude, and signal-to-noise ratio with typical noise types. Theoretical and experimental results show that the new method can be used in fine determination of the frequency if the user has prior knowledge of the approximate location of the frequency


