Various twofold symmetry-protected Weyl points in bosonic systems
Date:21-07-2020 Print
Nowadays, the study of the low-energy quasi-particles (the counterparts of the high-energy particles) in condensed matters is of great interest. The Weyl fermions are very stable and have topological Chern number. To search for Weyl points (WPs) is a challenge due to the requirement of comprehensive calculations in general. Although the WPs do not need symmetry protections, additional symmetries can pin a WP at a fixed point. As we know, in spinful electronic systems, time-reversal (TR) symmetry makes that all Kramers pairs at the time-reversal-invariant momenta are WPs in chiral crystals. Then, we will ask if these symmetry-enforced Weyl points can emerge in bosonic systems. If yes, it will largely lower the difficulty to search for WPs.
Very recently, the joint research group of Prof. Zhijun Wang (Institute of Physics, Chinese Academy of Sciences) and Prof. Hua-Hua Fu (School of Physics, Huazhong University of Science and Technology) have performed the symmetry analysis of all 230 (single-valued) space groups. They have given a complete list of the high-symmetry k-points, where the twofold WPs can be pinned and protected in bosonic systems (see Table 1 in Section A of the Supplementary Information). Their corresponding topological Chern numbers are given also. The results show that they can have Chern numbers of ±1 [i.e. (monopole) WPs], ±2 [i.e., double WPs] and ±4 [i.e., quadruple WPs, which have not been reported before], respectively. These results can guide future experiments in the study of various WPs.
In addition, at several k-points (denoted by *), only the two-dimensional irrep of WPs is allowed; namely, they are symmetry-enforced WPs, which are usually protected by nonsymmorphic crystal symmetry. Unlike the TR-enforced WPs in spinful electronic systems, where the WPs are usually buried in bulk states due to the weak strength of spin-orbit coupling, these nonsymmorphic-crystal-symmetry-enforced WPs in bosonic systems can be well exposed. Consequently, the associated surface arcs are long and robust, which can be easily probed in future experiments. We have checked all the symmetry-enforced WPs in the calculations of phonon spectra of materials. Taking K2Sn2O3 of space group 199 as an example, the two WPs of the same chirality at two nonequivalent P points are related by time-reversal symmetry. In particular, at ~17.5 THz, a spin-1 Weyl phonon is also found at H, since two Weyl phonons at P carrying a non-zero net Chern number cannot exist alone in the 3D BZ. The significant separation between P and H points makes the surface arcs long and clearly visible.
This study entitled “Symmetry-enforced Weyl phonons” was published on npj Computational Materials 6: 95 (2020) (DOI:s41524-020-00358-8). This work was supported by the National Science Foundation of China (Grants No. 11774104, 11504117, and 11274128) and the Strategic Priority Research Program of Chinese Academy of Sciences (XDB33000000).
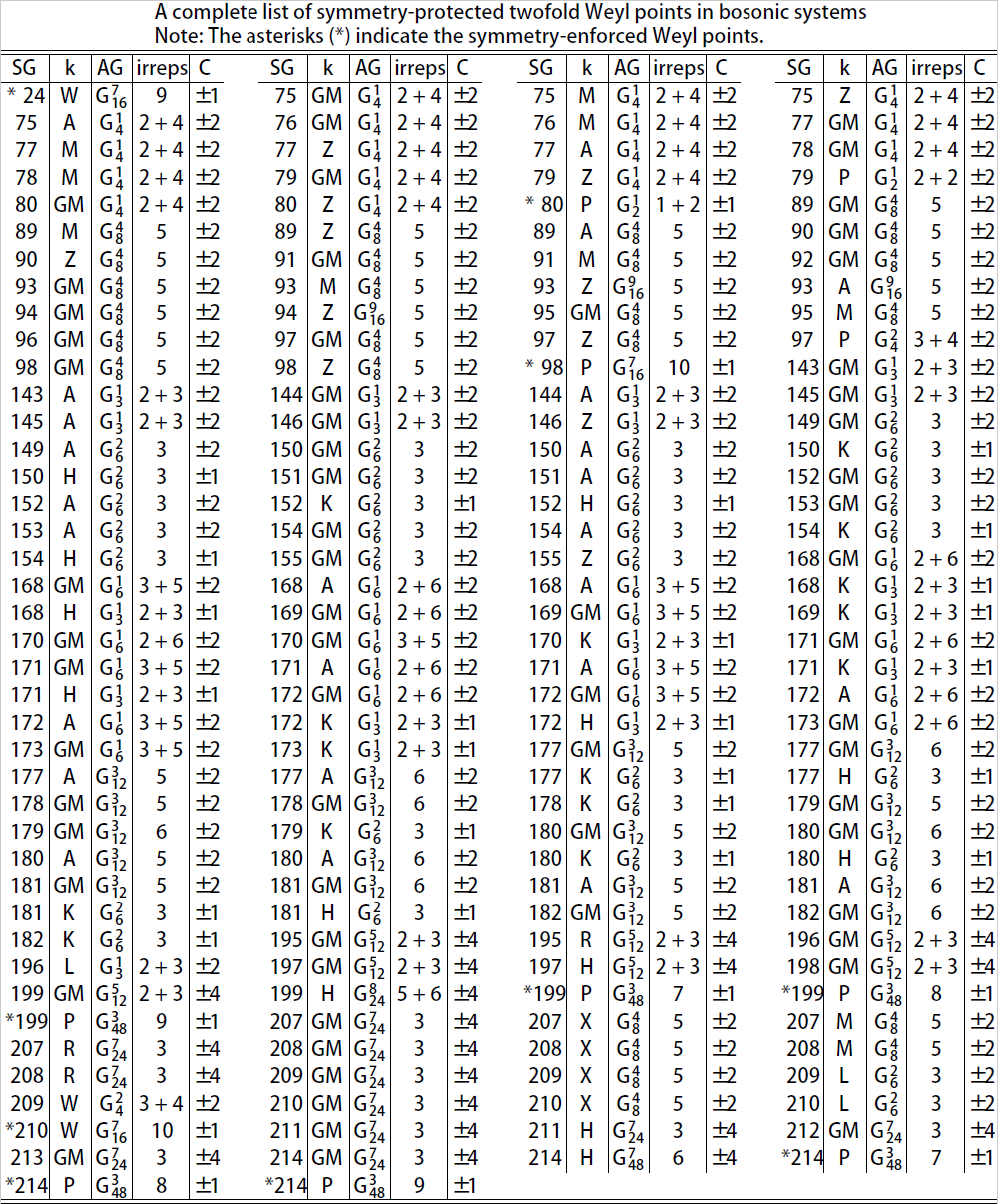
Table 1. A complete list of symmetry-protected two-fold Weyl points in bosonic systems. The first and the second columns indicate the space group (SG) number and the corresponding high-symmetry k-point. The third and fourth columns show the abstract group (AG), which the little group of the k-point is isomorphic with, and the corresponding irreps. The fifth column indicates the corresponding Chern numbers (C). The asterisks indicate the symmetry-enforced Weyl points.

Figure 1. The (110)-surface phonon dispersions and isofrequency surface contours in K2Sn2O3. a The surface phonon dispersions on the (110)-surface BZ of Fig. 1b. b-d The isofrequency surface contours at three different frequencies indicated by the three horizontal lines in a. e The distributions of two monopole WPs (P1 and P2 points) and the spin-1 WP (H point) in the first BZ. f The phonon dispersions of K2Sn2O3 along high-symmetry lines.
Contact:
Institute of Physics
Zhijun Wang
Email:wzj@iphy.ac.cn
Key word:
Twofold Weyl points; bosonic systems; symmetry protection; surface arc states.
Abstract:
In spinful electronic systems, time-reversal symmetry makes that all Kramers pairs at the time-reversal-invariant momenta are Weyl points (WPs) in chiral crystals. Here, we find that such symmetry-enforced WPs can also emerge in bosonic systems (e.g. phonons and photons) due to nonsymmorphic symmetries. We demonstrate that for some nonsymmorphic chiral space groups, several high-symmetry k-points can host only WPs in the phononic systems, dubbed symmetry-enforced Weyl phonons (SEWPs). The SEWPs, enumerated in Table 1, are pinned at the boundary of the three-dimensional (3D) Brillouin zone (BZ) and protected by nonsymmorphic crystal symmetries. By performing first-principles calculations and symmetry analysis, we propose that as an example of SEWPs, the twofold degeneracies at P are monopole WPs in K2Sn2O3 with space group 199. The two WPs of the same chirality at two nonequivalent P points are related by time-reversal symmetry. In particular, at ~17.5 THz, a spin-1 Weyl phonon is also found at H, since two Weyl phonons at P carrying a non-zero net Chern number cannot exist alone in the 3D BZ. The significant separation between P and H points makes the surface arcs long and clearly visible. Our findings not only present an effective way to search for WPs in bosonic systems, but also offer some promising candidates for studying monopole Weyl and spin-1 Weyl phonons in realistic materials.

