Quantum droplet with Borromean correlation
Date:14-10-2021 Print
Exploring dominant few-body correlations in many-body systems is one of the main tasks of modern physics, and the presence of exotic few-body bound states offers an efficient perspective to uncover the according few-body correlation in the many-body environment. In this aspect, the Borromean binding clearly belongs to such a case, where only three subjects are bound together while any two of them are unbound, analogous to the structure of Borromean ring in Fig.1. Typical examples of Borromean binding include the halo nuclei in 11Li and 6He, and the Efimov physics in the negative side of scattering length in ultracold atoms, both of which have been verified in experiments. Theoretical studies have also shown the Borromean trimer can be supported by fine-tuning the shape and strength of pairwise potential or by modifying the single-particle dispersion. Given the stringent requirement for its occurrence in small clusters, whether the Borromean binding can be extended to many-body systems due to collective effect is an interesting yet challenging problem. Addressing this problem will help to build up a bridge between the collective many-body effect and the quantum few-body correlation, thereby offering a new route for tackling the complicated many-body problems in strongly correlated systems.
On the other hand, the droplet represents a typical many-body bound state that has been well studied in literature, such as the helium liquid early from 1980’s. Recently, the droplet phase has regained great attention in ultracold atoms, and has been successfully observed in dipolar gases and the alkali two-species boson mixtures. Typically, the droplet holds a negative energy and zero pressure, and thus can be self-bound and stay in equilibrium with the vacuum. Its mechanism lies in a critical balance between the mean-field attraction and the Lee-Huang-Yang repulsion from quantum fluctuations. Then, an interesting question here is, will the droplet be stable under multi-component? And even further, can it support the intriguing Borromean binding?
Recently, Prof. Xiaoling Cui from the Institute of Physics, Chinese Academy of Sciences, together with the postdoc Yinfeng Ma and phD student Cheng has investigated the stability of quantum droplet in three-component boson mixtures and examined the possibility of Borromean binding therein. By analyzing the mean-field stability of this system under density fluctuations, they find that the stability regime of three-component system is always larger than that of two-component subsystems (see Fig.2), which means that the former can undergo mean-field collapse more easily than the latter. Its physical origin lies in the enhanced attractive force mediated by the density fluctuation of the third component. Such additional force intensifies the mean-field collapse of three-component system and facilitates the formation of quantum droplet after incorporating the repulsive force from Lee-Huang-Yang corrections. By definition, it is the Borromean droplet, where only three-component bosons can form the self-bound state while any two components cannot. They have identified the region of Borromean droplet in the phase diagram, as shown in Fig.3. Moreover, another interesting phenomenon is that outside the Borromean region, the three-component and two-component droplets can coexist in the form of phase separation, as manifested by the wedding cake structure in their density profile, see Fig.4.
These results have demonstrated that the three-component boson mixture can exhibit much richer physics than the two-component ones. This is the first study to extend the Borromean binding to the many-body world, and has shown the power of many-body collective effect in engineering bound states with a diversely fascinating structure. The work has been published recently in Phys. Rev. Lett. 127, 043002 (2021).
In addition, the same group has recently investigated the stability of quantum droplet under a uniform confinement. They showed that the confinement-induced boundary effect can be significant when increasing the atom number or reducing the confinement length, which destabilizes the quantum droplet towards the formation of a soliton bound state (see the phase diagram in Fig.5). This study has revealed the competition and coexistence of different bound states (droplet and soliton) in quasi-low-dimension, which can serve as a theoretical guide for detecting related phenomena in realistic experiments in near future. The according work has recently been published as a Letter in Phys. Rev. Research 3, L012027 (2021).
These studies are supported by the National Key Research and Development Program of China (2016YFA0300603, 2018YFA0307600), the National Natural Science Foundation of China (No.12074419), and the Strategic Priority Research Program of Chinese Academy of Sciences (No. XDB33000000).
Link:
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.127.043002
https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.3.L012027

Fig.1: Borromean ring:only three rings can be linked together while any two of them are unlinked.

Fig.2:Mean-field stability diagram of three-component bosons. The gray area is the stable region, which is smaller than the stable region of two-component ones (surrounded by red dashed lines).
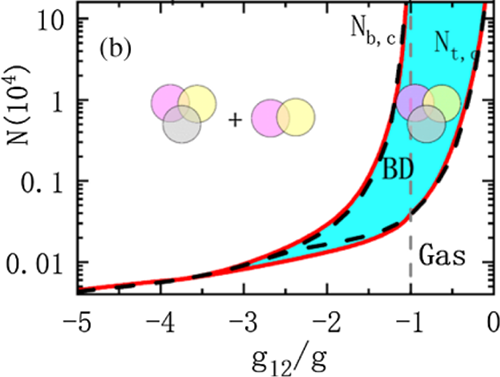
Fig.3: Phase diagram in the parameter plane of particle number and interaction strength. The blue area marks the region of Borromean droplet (“BD”). Below and above this region are, respectively, the gas phase and the droplet-coexistence phase.

Fig.4: Phase separation of three-component and two-component droplets.
 (a)
(a) (b)
(b)
Fig.5: (a) Illustration of confinement-induced bound effect: when increase the particle number or reduce the trap length, the droplet can become unstable when its size is comparable to the trap length. (b) Phase diagram in the parameter plane of particle number and trap length. The blue and white areas marks, respectively, the droplet and soliton regions, and the gray area is the region when these two states can coexist with each other.


