Scientists Reveal a Linear Relation between Radiative and Nonradiative Decay Rates of Molecules
Date:17-05-2023 Print
Efficient fluorescent molecules have extensive applications in fields such as molecular biological imaging, organic light-emitting diodes and laser applications. The fluorescence efficiency of molecules depends on two competing relaxation processes of the excited state, namely radiative and nonradiative transitions. Radiative transitions involve the emission of a photon with energy equal to or less than the excitation energy, whereas nonradiative channels transfer excitation energy to the vibrational levels without any photon emission. The ratio of the radiative decay rate (kR) to the nonradiative decay rate (kNR) determines the fluorescence quantum yield of the molecule. Research on radiative and nonradiative transitions has been ongoing for many years, and the theoretical framework for each process is well established. For the radiative decay rate of fluorescent molecules, the dominant factor is generally the electronic coupling elements. For the nonradiative decay rate, the focus of researchers has mainly been on the vibrational coupling elements, resulting in the energy gap law stating that a larger energy difference between the excited and ground states leads to slower vibrational relaxation. Besides, the electronic coupling elements of kNR is often treated as a computational constant. Although some important work has explored the correlation between the two rates, a clear relationship between their electronic coupling terms has not been well established. In 1981, SIEBRAND et al. (Chem. Phys. Lett. 1981, 80, 399-403) proposed an electronic propensity rule based on the interaction between the internal electric field and the external radiation field. This rule indicates that in a series of related molecules or comparable states of the same molecule when the radiative rate constants increase, the rates of competing nonradiative decay processes would increase correspondingly. In other words, for given molecules and electronic states, the ratio of the contributions of the electronic coupling terms to kR and kNR is fixed. To increase the quantum efficiency of the molecule, the contribution of the vibrational coupling to the nonradiative transition rate must be reduced. This rule provides a guiding principle for the rational design of high quantum yield fluorescent molecules. However, so far, the electronic propensity rule lacks rigorous theoretical derivation and experimental verification. In 1984, SCHUURMANS and van DIJK (Physica B & C 1984, 123, 131-155) provided the ratio of kR and kNR in rare earth metal crystals under weak electron-phonon coupling at low temperature (0 K). Based on the commutativity of quantum mechanical operators, they derived the proportionality between the electronic coupling terms for kR and kNR, revealing the inherent correlation between electronic state interactions for radiative and nonradiative transitions. However, how to apply this proportionality relationship to molecular systems and establishing a universally applicable relationship that can be experimentally verified at high temperatures (room temperature) requires further theoretical derivation and experimental design.
On April 28th, 2023, the Journal of Physical Chemistry Letters published an online report on the research work conducted by the WENG Yuxiang research group in Soft Matter Physics Laboratory (SM06) at the Institute of Physics, Chinese Academy of Sciences/Beijing National Laboratory for Condensed Matter Physics. The letter is titled "Theoretical and Experimental Investigation of the Electronic Propensity Rule: A Linear Relation between Radiative and Nonradiative Decay Rates of Molecules" (Figure 1). The doctoral students ZHANG Ying and LIU Heyuan are the first and second authors, respectively.
This work summarized the theoretical derivation of kR and kNR by SCHUURMANS et al. The electronic coupling term in kR is the electronic dipole moment (\(\boldsymbol{\mu}=\boldsymbol{\Sigma}_e e \boldsymbol{r}_e\)) acting on the electronic wave functions of the excited and ground states of the molecule. In contrast, for kNR the differential operator of the normal vibrational coordinates (Qk, a linear combination of nuclear coordinates Ran) acts on the electronic wave functions of the excited and ground states. Specifically:
\(J\left(k_R\right) \propto\left\langle\phi_f\left|e \boldsymbol{r}_e\right| \phi_i\right\rangle_e ; J\left(k_{N R}\right) \propto\left\langle\phi_f\left|\frac{\partial}{\partial R_{a n}}\right| \phi_i\right\rangle_e\).
Formally, the two are not directly related. SCHUURMANS et al. introduced the velocity expression of the electronic dipole operator, given by CHANDRASEKHAR X.:
\(\left\langle\phi_f|\boldsymbol{\mu}| \phi_i\right\rangle_e=\frac{e \hbar^2}{m_e \mit\Delta E}\left\langle\phi_f\left| \boldsymbol{\Sigma}_e \boldsymbol{\nabla}_{r_e}\right| \phi_i\right\rangle_e\).
By specifying the symmetry of the molecular internal interaction potential on the electronic and nuclear coordinates \(\boldsymbol{\Sigma} _e \boldsymbol{\nabla}_{r_e} V(\boldsymbol{r}, \boldsymbol{R})+\boldsymbol{\Sigma} _n \boldsymbol{\nabla}_{R_n} V(\boldsymbol{r}, \boldsymbol{R})=0\), and performing the commutativity of quantum mechanical operators, the equivalent relationship between the electronic coordinate gradient operator and the nuclear coordinate gradient operator acting between the initial and final electronic states was obtained, i.e., \(\left\langle\phi_f \mid \Sigma_e \nabla_{r_e} \phi_i\right\rangle_e=-\left\langle\phi_f \mid \Sigma_n \nabla_{R_n} \phi_i\right\rangle_e\). This established the inherent connection between the electronic coupling terms for radiative and nonradiative transitions, allowing for the ratio of kR to kNR to be obtained at 0 K. To meet the requirement of high symmetry for molecular internal interaction potential, ZHANG et al. introduced the single-electron approximation, making Schuurmans' theoretical work more comprehensive and applicable to fluorescent molecules.
To verify the relationship between kR and kNR in experiments, the research team further investigated the effect of external electric fields on kR and kNR. They used the polarizable continuum model (PCM) to explore the effect of the external electric field on the molecular Coulomb potential. Within this theoretical framework, the electric field perturbation caused by changes in the solvent environment can cause corresponding changes in kR and kNR, but the ratio between the two remains unchanged. In addition, the work introduced the theoretical work of Professor LIN S. H. (J. Chem. Phys. 1972, 56, 2648-2653) on the effect of temperature on nonradiative decay rates and obtained finally a linear relationship between kR and kNR at higher temperatures (room temperature). Based on their theory, the team designed an experiment to control the molecular kR and kNR by changing the dielectric constant of the solution at room temperature and to verify the linear relationship derived from theory. By measuring kR and kNR of the dextran-dye molecules and the photosynthetic bacterial light-harvesting antenna protein complexes (LH2) in salt solutions of different concentrations, the team obtained experimental results consistent with the expected linear relationship (Figure 2).
This work provides a theoretical understanding of the linear relation between radiative and nonradiative decay rates of molecules under external electric field perturbation in weak coupling limit, and verifies this relationship through experimental data from dextran-dye molecules and LH2. This work provides further insights into the relationship between radiative and nonradiative processes and has some theoretical guidance for the efficiency of molecular luminescence, among other applications.
The study was supported by the Ministry of Science and Technology, the National Natural Science Foundation of China, the Strategic Priority Research Program of the Chinese Academy of Sciences, and the Chinese Academy of Sciences Frontier Science Key Programs.
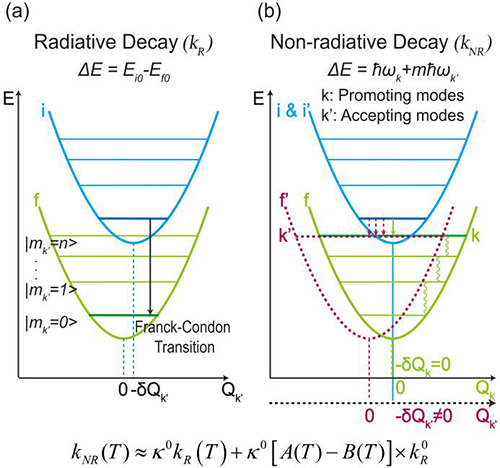
Figure 1. Schematic representation of the radiative and nonradiative decay processes in weak coupling limit. (a) Radiative process releasing a photon without phonons. (b) Nonradiative processes for energy relaxation by promoting modes and accepting modes. (Image by Institute of Physics)
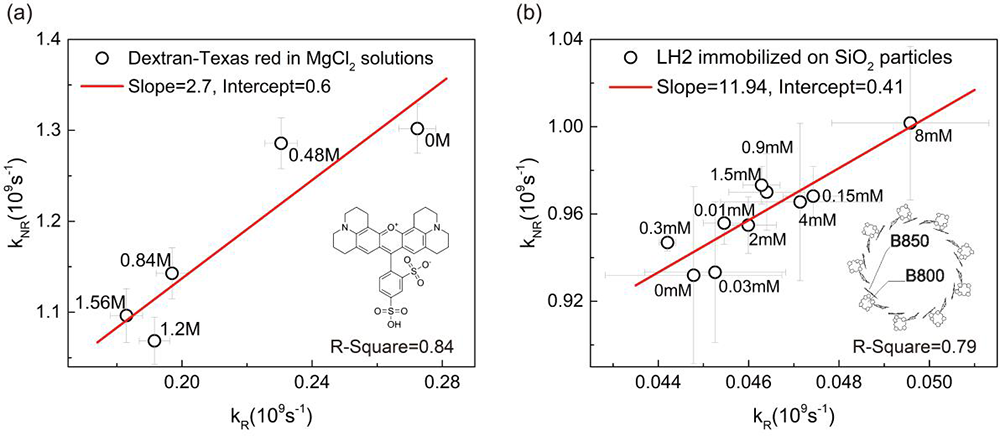
Figure 2. Plot of kNR against kR for (a) dextran-Texas red in MgCl2 solutions of different concentrations, and (b) LH2 adsorbed on 4 nm SiO2 nanoparticles at different concentrations of NaCl. (Image by Institute of Physics)
Contact:
Institute of Physics
WENG Yuxiang
Email: yxweng@iphy.ac.cn
Key words:
Fluorescence efficiency; radiative decay rate; nonradiative decay rate; electronic propensity rule
Abstract:
This study provides a theoretical derivation of a linear relation between radiative and nonradiative decay rates of molecules under external electric field perturbation in weak coupling limit, and verifies this relationship through experimental data from dextran-dye molecules and the photosynthetic bacterial light-harvesting antenna protein complexes.

