A Universal Method to Predict Critical Points in Magnetic Systems
Date:13-11-2025 Print
The physical process of transition between one state of a medium and another is called phase transition. As a common phenomenon in nature, phase transitions widely exist in physical systems, biological networks, and social systems. Depending on whether the factors causing the phase transition originate from in or outside the system, phase transitions can be classified as equilibrium and non-equilibrium phase transitions. The former corresponds to phase transitions driven by internal forces, while the latter corresponds to those driven by external forces. Accurately predicting the critical point of a phase transition is crucial for avoiding system collapse and reducing experimental and computational costs. However, the complexity of physical systems and phase transition phenomena has long made research methods for determining critical points highly specific and lacking generality. Equilibrium and non-equilibrium phase transitions exhibit significant differences in mechanisms, behaviors, and research approaches, and a unified method for determining critical points has long been absent. Magnetic systems, due to their clear physical representations of both types of phase transitions, serve as an ideal platform for studying this issue.
Recently, Ph.D. student Tianyi Zhang, Associate Professor Caihua Wan, and Professor Xiufeng Han from the M02 group of the State Key Laboratory of Magnetism, Institute of Physics, Chinese Academy of Sciences, proposed a universal indicator for predicting critical points based on the frequency-dependent response function. This indicator is applicable to both equilibrium and non-equilibrium magnetic phase transition systems. The magnetic moment can be switched using either a magnetic field or a spin torque — the former corresponds to equilibrium phase transitions, while the latter corresponds to non-equilibrium phase transitions. In the case of magnetic moment switching driven by a magnetic field Bz (Fig. 1a), a horizontal perturbation field Bx0 cos(ωt) is applied. The relationship between the peak value of the horizontal component of the magnetic moment mx, the magnetic field Bz, and the frequency ω is shown in Fig. 1b. As Bz approaches the critical point Bc, the static (ω = 0) response function tends to diverge in an inverse proportionality form, while the dynamic (ω = ωc, the intrinsic magnetic resonance frequency) response function gradually decreases (Fig. 1c). Therefore, the static response function can serve as a predictor for the magnetic moment switching process driven by a magnetic field. In the case of spin-torque-driven magnetic moment switching (Fig. 1d), the relationship between the peak value of mx, the spin torque Jstt, and the frequency ω is shown in Fig. 1e. As Jstt approaches the critical point Jc, the dynamic (ω = ωc) response function tends to diverge in an inverse proportionality form, while the static (ω = 0) response function gradually decreases (Fig. 1f). Hence, the dynamic response function can serve as a predictor for spin-torque-driven magnetic moment switching. Further studies reveal that these static and dynamic indicators can be unified within the framework of a first-order linear differential system, providing a generalizable strategy for predicting critical points in both equilibrium and non-equilibrium phase transitions.
The study of predictive indicators for critical points in equilibrium and nonequilibrium phase transitions within magnetic systems provides new insights for understanding phase transition phenomena in nature and exploring their universal principles, while also demonstrating the extensible potential of this approach in interdisciplinary research. This work holds promising applications in spintronics, including criticality-enhanced magnetic sensors, uniformity testing of magnetic memory devices, dynamic control of spin-torque oscillators, and design of novel magnetic materials. The findings, entitled "Predictive Indicator of Critical Point in Equilibrium and Nonequilibrium Magnetic Systems" have been published in Physical Review Letters. Tianyi Zhang, Ph.D. student from the M02 group at the Institute of Physics, Chinese Academy of Sciences, is the first author, while Associate Professor Caihua Wan and Professor Xiufeng Han are corresponding authors. This research is supported by the National Key Research and Development Program of China (MOST), the National Natural Science Foundation of China (NSFC), and the Chinese Academy of Sciences President’s International Fellowship Initiative.
Contact:
Institute of Physics
Han Xiufeng
Email:xfhan@iphy.ac.cn
Key words:
Magnetic phase transitions, Spin dynamics, Response function, Nonequilibrium systems
Abstract:
The frequency-dependent response function can be used as a general predictor for the critical points of both equilibrium and non-equilibrium magnetic phase transitions, and this indicator can be extended to systems whose dynamics satisfy the first-order linear differential equations.
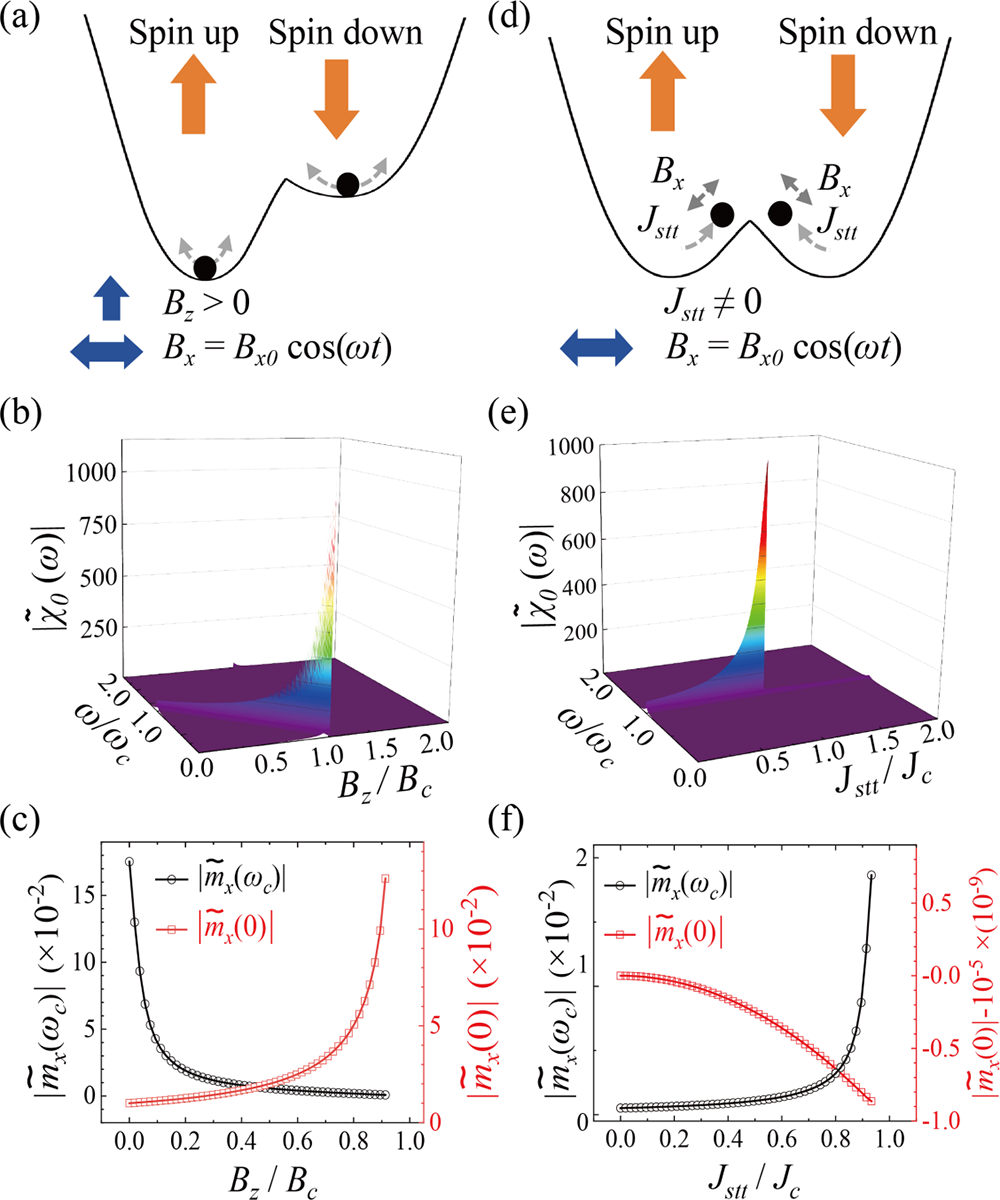
Figure 1: Schematic diagrams and predictive indicators for phase transitions in equilibrium and nonequilibrium magnetic systems. (a) Double-well energy landscape illustrating magnetic moment switching driven by a magnetic field. (b) Dependence of the response function on the DC magnetic field and the frequency of the AC perturbation field. (c) Divergence of the static response function near the critical magnetic field. (d) Double-well energy landscape illustrating magnetic moment switching driven by spin torque. (e) Dependence of the response function on the DC current and the frequency of the AC perturbation field. (f) Divergence of the dynamic response function near the critical magnetic field.


