Directional Scaling Symmetry Revealed in High-symmetry Two-dimensional Lattices
Date:30-09-2014 Print
Geometrical transformation includes mirror reflection, rotation, glide and scaling, yet in dealing with the geometrical transformation of space lattices, only mirror reflection, rotation, glide are considered. Scaling symmetry is often neglected as it is notorious for its non-existence in most geometrical structures, a fact noticed and discussed by Galileo.
Two-dimensional high-symmetry lattices provide the arena for many physics problems of essential importance. A scale symmetry cannot be excluded in such lattices, as there are already 17 space groups for the 2D lattices. In the search of single tiling scheme for the 12-fold quasiperiodic structure(J. Phys. A: Math. Theor. 46,245205 (2013)), Dr. Liao Longguang and Prof. Cao Zexian, Institute of Physics, CAS, were led to the study of the function y = arcsin(sin(2πxn)), where the parameter x is either the platinum number 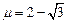 or the silver number
or the silver number 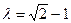 , which are related to the 12-fold and 8-fold quasiperiodic structures, respectively. They found that the plots of the functions for
, which are related to the 12-fold and 8-fold quasiperiodic structures, respectively. They found that the plots of the functions for 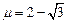 and
and 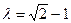 can be taken as the Moiré pattern of the two overlapping, roughly speaking, equilateral triangular lattices or square lattices when the ordinate and the abscissa are appropriately scaled. By studying the variation of the patterns with the scale, directional scaling symmetry of the square lattice and the equilateral triangular lattice is revealed. With the drag center set on a lattice point, in the case of equilateral triangular lattice, the direction of scaling symmetry is at 15°with regard to the side of the unit triangle, and the scale factor is
can be taken as the Moiré pattern of the two overlapping, roughly speaking, equilateral triangular lattices or square lattices when the ordinate and the abscissa are appropriately scaled. By studying the variation of the patterns with the scale, directional scaling symmetry of the square lattice and the equilateral triangular lattice is revealed. With the drag center set on a lattice point, in the case of equilateral triangular lattice, the direction of scaling symmetry is at 15°with regard to the side of the unit triangle, and the scale factor is  , while in the case of square lattice, the direction of scaling symmetry is at 22.5°with regard to the side of the unit square triangle, and the scale factor is
, while in the case of square lattice, the direction of scaling symmetry is at 22.5°with regard to the side of the unit square triangle, and the scale factor is 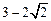 (Sci. Rep. 4, 6193 (2014)).
(Sci. Rep. 4, 6193 (2014)).
Further, Prof. Cao studied the directional scaling symmetry in the equilateral triangular lattice and square lattice, by representing the lattices with the Eisenstein integers or Gaussian integers. It is found that there exist infinitely more directional scaling symmetries for the square lattice: Along any direction, through a lattice point, at an angle θ ( 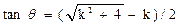 , k=1,2,3…….) with respect to the neighboring edge of the unit cell, the lattice displays a directional scaling symmetry, and the scale factor is given by tan2θ . For the case of k = 1 ,
, k=1,2,3…….) with respect to the neighboring edge of the unit cell, the lattice displays a directional scaling symmetry, and the scale factor is given by tan2θ . For the case of k = 1 , 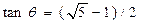 which is the golden ratio.
which is the golden ratio.
The directional scaling symmetry for the equilateral triangular lattice and square lattice, and their relation to the golden ratio, silver ratio and platinum ratio, are expected to have some impact on the various physics problems, particularly in statistical physics, condensed matter physics, quantum field theory, etc., modeled on high-symmetry 2D lattices. The scaling symmetry of a lattice will be incorporated into the Hamiltonian for a quantum model defined on it, which in turn will determine the feature of ground energy degeneracy-a pivotal concept for the discussion of quantum critical phenomenon. Remarkably, the golden ratio 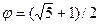 , has been found lying beneath many fundamental physical problems, and usually in unexpected places. For instance, the lowest two masses of the bound states, m1 and m2, in the 1D Ising model realized in CoNb2O6 crystal, have the ratio m1 / m2 = φ, as predicted by E8 Lie group. The critical fugacity for the hard-hexagon model is found to be Zc = φ5, while the maximum of Hardy’s probability, a quantity referring to the Hardy’s test of Bell’s inequality, for quantum system of arbitrary finite dimension is PHardy = 1/φ5. Such observations have not yet been well understood. It is anticipated by analogy that the silver ratio and the platinum ratio may also be found relevant in some physical problems defined on such lattices.
, has been found lying beneath many fundamental physical problems, and usually in unexpected places. For instance, the lowest two masses of the bound states, m1 and m2, in the 1D Ising model realized in CoNb2O6 crystal, have the ratio m1 / m2 = φ, as predicted by E8 Lie group. The critical fugacity for the hard-hexagon model is found to be Zc = φ5, while the maximum of Hardy’s probability, a quantity referring to the Hardy’s test of Bell’s inequality, for quantum system of arbitrary finite dimension is PHardy = 1/φ5. Such observations have not yet been well understood. It is anticipated by analogy that the silver ratio and the platinum ratio may also be found relevant in some physical problems defined on such lattices.
This research is spontaneous and serendipitous.
Link: http://www.nature.com/srep/2014/140826/srep06193/full/srep06193.html
http://iopscience.iop.org/1751-8121/46/24/245205/article
 |
Fig.1. Plots of the sinusoidal functiony= sin(2πμn)(a) and the arcsine function y= arcsin(sin(2πμn))(b), where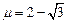 , and the argument n is non-negative integer. , and the argument n is non-negative integer. |
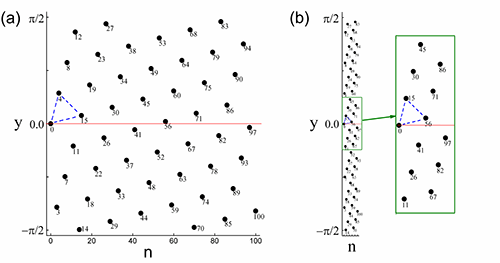 |
Fig.2. (a) Plot of the ascending branch of the functiony= arcsin(sin(2πμn)), where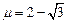 , and n is non-negative integer, which forms approximately a triangular lattice; (b) The result of scaling along the horizontal axis with a scale factor of ~ , and n is non-negative integer, which forms approximately a triangular lattice; (b) The result of scaling along the horizontal axis with a scale factor of ~ . Points are indexed with the corresponding argument n. . Points are indexed with the corresponding argument n. |
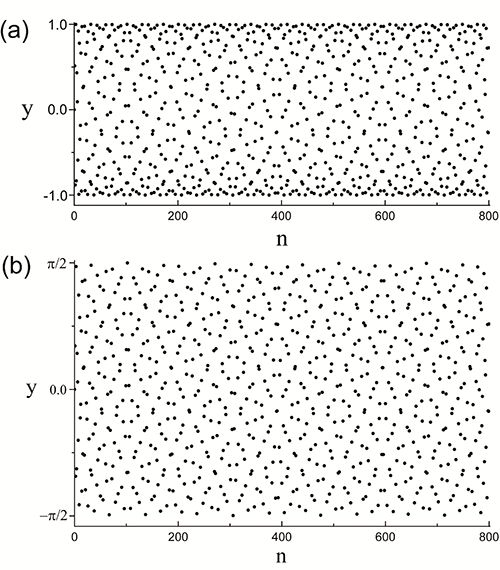 |
Fig.3. Plots of the sinusoidal functiony= sin(2πλn) (a) and the arcsine functiony= arcsin(sin(2πλn))(b), where 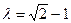 , and the argument n is non-negative integer. , and the argument n is non-negative integer. |
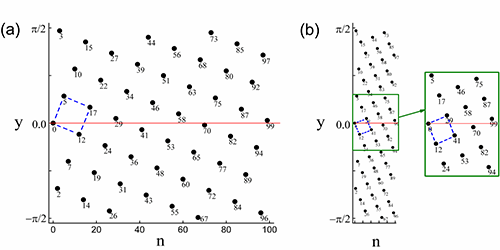 |
Fig.4. (a) Plot of the ascending branch of the functiony= arcsin(sin(2πλn)), where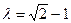 , and n is non-negative integer, which forms approximately a square lattice; (b) The result of scaling along the horizontal axis with scale factor ~ , and n is non-negative integer, which forms approximately a square lattice; (b) The result of scaling along the horizontal axis with scale factor ~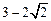 . Points are indexed with the corresponding argument n. . Points are indexed with the corresponding argument n. |

