Emmy Noether looks at the deconfined quantum critical point
Date:24-05-2019 Print
The deconfined quantum critical point (DQCP) describes a continuous phase transition between two phases that spontaneously breaks different symmetries [1]. Outside the realm of the Landau-Ginzburg-Wilson paradigm of phase transitions which is based on the concept of order parameter, the DQCP represents the new paradigm of quantum matter which manifests the concepts of fractionalized excitations (spinons in the model realization of the DQCP – the JQ model [2,3]) and emergent gauge structure and symmetry [4].
However, there still exist ambiguities in the presence of the emergent continuous symmetry at the DQCP. Up to now several numerical methods have been employed, including comparing the critical exponents in different phases and plotting the order parameter histograms at the critical point, but due to the limited numerical accuracy, these results could offer indirect evidence of the existence of emergent continuous symmetries at DQCP. The conserved Noether current that is directly associated with the existence of continuous symmetry has not been tested till now.
Recently, Dr. Nvsen Ma and Prof. Zi Yang Meng from Institute of Physics, Chinese Academy of Sciences and assistant Prof. Yizhuang You from University of California at San Diego investigated the emergent symmetry at DQCP on the two dimensional easy-plane JQ model (shown in Fig.1), inspired by the power and conciseness of the Noether’s theorem [5]. The theorem states that every continuous symmetry of a physical system is associated with a corresponding conservation law. The conservation law further manifests itself in the form of a conserved current. Likewise, the observation of a conserved current in a physical system is the direct evidence of the existence of the associated continuous symmetry. These researchers constructed the currents operators in the field theoretical description of the DQCP with emergent O(4) symmetry and found their corresponding operators in the lattice model realization, as shown in the Table 1. Among all the current operators, they found that J^23 – the spin operator Sx at momenta (pi,0) – is the most important one in testing the emergent O(4) symmetry in this microscopic system.
With such understanding, these researchers performed large-scale quantum Monte Carlo simulations on the model to test their ideas. They measured the dynamical spin correlation functions at the corresponding momenta, and found that the scaling dimension of J^23 is indeed converged to the integers only related with the space-time dimension of the problem with no renomalization corrections – the unique property of conserved current operator. They also tested another conserved current J^34 using same method, which is the Sz correlation at momenta (0,0). The simulation results in Fig. 2 show that the correction of the scaling dimension eta of both currents indeed extrapolated to zero at the infinite size limit, which presents a direct evidence for the emergent O(4) symmetry.
The idea of employing conserved current to detect the emergent continuous symmetry is generic, the work [5] has already inspired another recent work in a one dimensional spin system with emergent continuous symmetry [6].
The related work titled "Role of Noether’s Theorem at the Deconfined Quantum Critical Point" is published in the latest issue of Phys. Rev. Lett.122,175701 (2019).
 |
| Figure 1:Easy-Plane JQ model and the deconfined quantum critical point. |
 |
| Figure 2:Correspondence of the current operators in the microscopic lattice model and field theoretical description. |
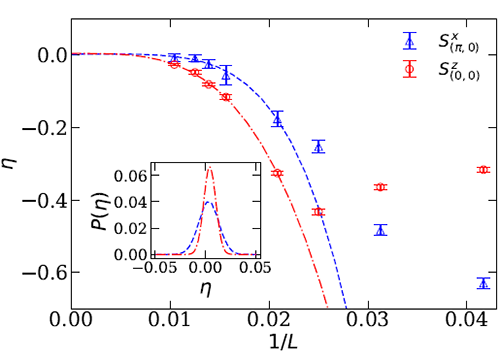 |
| Figure 3: The conserved currents discovered in quantum Monte Carlo simulations. The eta is the correction of the scaling dimension of the operators and at the thermodynamic limit of L going to infinity, the eta of the two current operators extrapolates to zero. |
Acknowledgement
The large-scale simulations are performed on the Tianhe-1A platform at the National Supercomputer Center in Tianjin and Tianhe-2 platform at the National Supercomputer Center in Guangzhou, the authors acknowledge the technical support and generous allocation of CPU time from these centers. The authors also thank the funding support from the Ministry of Science and Technology of China through the National Key Research and Development Program (2016YFA0300502), the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB28000000), the National Science Foundation of China (11574359, 11674370) and the DFG research unit FOR1807 and Mercator Fellow.
References
[1] Quantum criticality beyond the Landau-Ginzburg-Wilson paradigm, T. Senthil, Leon Balents, Subir Sachdev, Ashvin Vishwanath, and Matthew P. A. Fisher, Phys. Rev. B 70, 144407(2004)
[2] Evidence for Deconfined Quantum Criticality in a Two-Dimensional Heisenberg Model with Four-Spin Interactions, Anders W. Sandvik, Phys. Rev. Lett. 98, 227202 (2007)
[3] Duality between the Deconfined Quantum-Critical Point and the Bosonic Topological Transition, Yan Qi Qin, Yuan-Yao He, Yi-Zhuang You, Zhong-Yi Lu, Arnab Sen, Anders W. Sandvik, Cenke Xu, and Zi Yang Meng, Phys. Rev. X 7, 031052(2017)
[4] Dynamical signature of fractionalization at a deconfined quantum critical point, Nvsen Ma, Guang-Yu Sun, Yi-Zhuang You, Cenke Xu, Ashvin Vishwanath, Anders W. Sandvik, and Zi Yang Meng, Phys. Rev. B 98, 174421 (2018) Editors' Suggestion
[4] Quantum phases of SrCu2(BO3)2 from high-pressure thermodynamics, Jing Guo, Guangyu Sun, Bowen Zhao, Ling Wang, Wenshan Hong, Vladimir A. Sidorov, Nvsen Ma, Qi Wu, Shiliang Li, Zi Yang Meng, Anders W. Sandvik, Liling Sun, arXiv:1904.09927
[5] Role of Noether’s Theorem at the Deconfined Quantum Critical Point, Nvsen Ma, Yi-Zhuang You, and Zi Yang Meng, Phys. Rev. Lett. 122, 175701 (2019) https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.122.175701
[6] Emergent Symmetry and Conserved Current at a One Dimensional Incarnation of Deconfined Quantum Critical Point, Rui-Zhen Huang, Da-Chuan Lu, Yi-Zhuang You, Zi Yang Meng, Tao Xiang, arXiv:1904.00021


